Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
* Hướng dẫn giải: Đơn giản ta có được
S 1 = 3 ( 4 πr 2 ) = 12 πr 2 , S 2 = 12 πr 2
⇒ S 1 S 2 = 1

Chọn A.
Gọi r là bán kính quả banh. Ta có:
S 1 = 3 4 πr 2 = 12 πr 2
S 2 = 2 πr . 6 r = 12 πr 2

Hạ đường sinh AA1 vuông góc với đáy chứa cạnh CD. Khi đó góc ADA1 là góc giữa hai mặt phẳng hình vuông và mặt đáy.
Vì góc A1DC = 1v nên A1C là đường kính.
Gọi cạnh hình vuông là a.
Ta có
a2 = AD2 = AA12 + A1D2
mà AA1 = h = r, nên ta có:
A1D2 + DC2 = A1C2;
a2 – r2 + a2 = 4r2;
⇒a2=52r2
Vậy diện tích hình vuông là: SABC=a2=52r2 Gọi δ = góc ADA1 là góc tạo bởi mặt phẳng hình vuông và đáy, ta có: sinδ = A1AAD=ra=√25
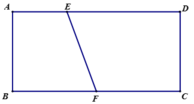
Gọi C C 1 và D D 1 là hai đường sinh của khối trụ
Khi đó D 1 C 1 / / = D C (1)
Đông thời ABCD là hình vuông nên AB//=DC (2)
Từ (1) và (2) suy ra AB//= D 1 C 1
Vậy A B C 1 D 1 nội tiếp đường tròn (O) nên A B C 1 D 1 là hình chữ nhật. Suy ra A C 1 là đường kính của (O)
Nghĩa là A C 1 = 2 r
Tam giác A B C 1 vuông ở B nên:
![]() (3)
(3)
Tam giác B C C 1 vuông ở C 1 nên:
![]() (4)
(4)
Từ (3) và (4) suy ra
![]()
Vậy diện tích hình vuông ABCD là S = A B 2 = 5 r 2 2
* Gọi α là góc hợp bởi mp(ABCD) và mặt phẳng đáy của hình trụ, ta có:
![]()
Với 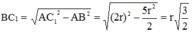
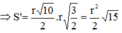
Mà A B C 1 D 1 là hình chiếu của ABCD trên mặt đáy hình trụ nên:
S
'
=
S
.
cos
α
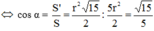

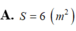
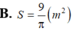
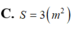
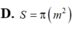





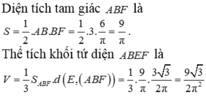

Chọn đáp án B.
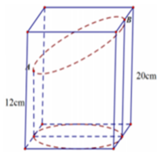
Hộp hình trụ có R = h = 10. Gọi a là độ dài cạnh hình vuông (tấm bìa) đã cho. Gọi AB, CD lần lượt là cạnh hình vuông trên mặt đáy; cạnh trên mặt phía trên của hộp. Gọi E, F lần lượt là hình chiếu vuông góc của C, D xuống mặt đáy.
Ta có: E F = C D = A B E F / / C D / / A B
⇒ A E F B là hình chữ nhật nội tiếp đường tròn có bán kính R = 10 .
Do đó A B 2 + B F 2 = A F 2
⇔ A B 2 + B F 2 = 4 R 2 ⇔ a 2 + B F 2 = 4 R 2 ( 1 )
Mặt khác theo pitago có:
B D 2 = B F 2 + F D 2 ⇔ a 2 = B F 2 + h 2 ( 2 )
Từ (1) và (2) có:
4 R 2 - a 2 = a 2 - h 2 ⇔ a 2 = h 2 + 4 R 2 2 = 10 2 + 4 × 10 2 2 = 250