Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
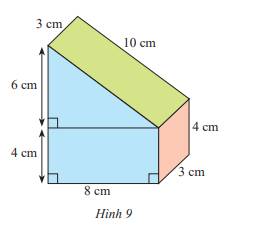
Thể tích của cái bánh là thể tích của hình lăng trụ tam giác, đáy là tam giác vuông có hai cạnh góc vuông bằng 6cm và 8 cm.
Thể tích hình lăng trụ là:
\(V = \left( {\frac{1}{2}.6.8} \right).3 = 72\left( {c{m^3}} \right)\)
b)
Diện tích vật liệu cần dùng là tổng diện tích xung quanh hình lăng trụ + diện tích hai mặt đáy.
Diện tích xung quanh hình lăng trụ đứng tam giác là:
\({S_{xq}}\) = Cđáy.h = (6 + 8 + 10).3 = 72 (cm2)
Diện tích vật liệu cần dùng là:
\(S_{xq} + 2S_{đáy} = 72 + 2.\frac{1}{2}.6.8 = 120\left( {c{m^2}} \right)\)

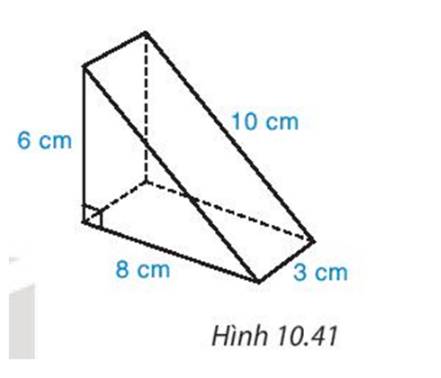
Diện tích xung quanh chiếc hộp là:
Sxq = Cđáy . h = (6+4+8+4+10).3 = 96 (cm2)
Diện tích đáy là:
Sđáy = (10+4).8 : 2 = 56 (cm2)
Diện tích phần cần sơn là:
96 + 56 = 152 (cm2)

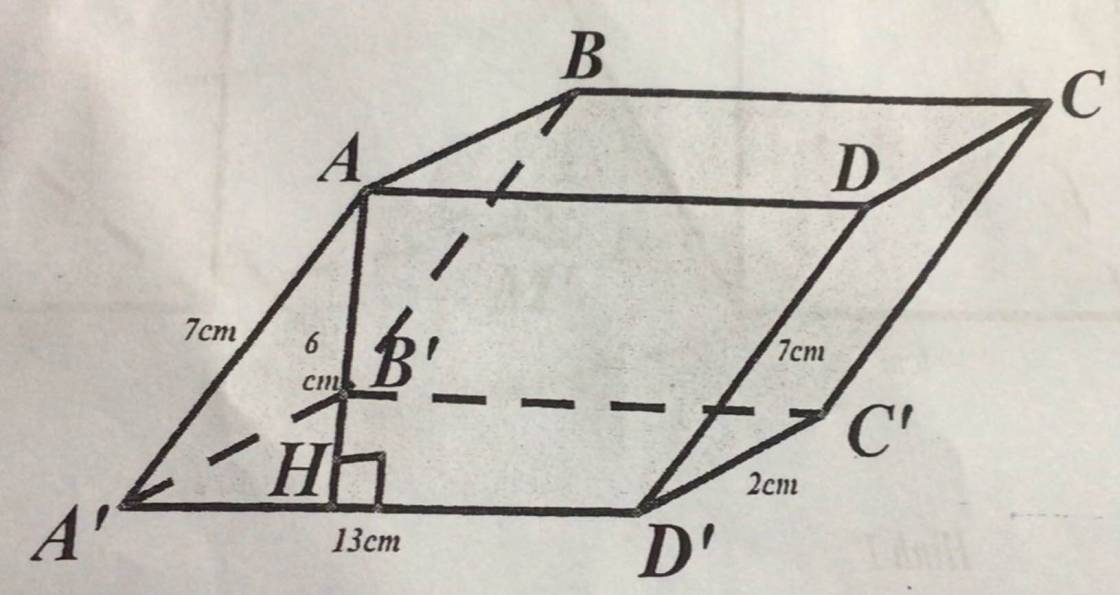
Ta có Sxq= chu vi đáy (hình bình hành) nhân chiều cao= 2.(7+13).2=80 cm vuông
Ta có V(thể tích)= S đáy . Chiều cao=6.13.2=156 cm khối
Chúc bạn học tốt và nhớ đọc kỹ kiến thức trong sách giáo khoa

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

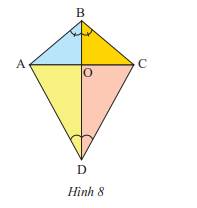
a) Tia BO là tia phân giác của \(\widehat {ABC}\) vì tia BO nằm giữa 2 tia BA và BC, tạo với 2 cạnh BA và BC 2 góc bằng nhau.
Tia DO là tia phân giác của \(\widehat {ADC}\) vì tia DO nằm giữa 2 tia DA và DC, tạo với 2 cạnh DA và DC 2 góc bằng nhau
b) Vì BO là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {ABO} = \widehat {CBO} = \frac{1}{2}.\widehat {ABC} = \frac{1}{2}.100^\circ = 50^\circ \)
Vì DO là tia phân giác của \(\widehat {ADC}\)nên \(\widehat {ADO} = \widehat {CDO} = \frac{1}{2}.\widehat {ADC} = \frac{1}{2}.60^\circ = 30^\circ \)
Vậy \(\widehat {ABO} = 50^\circ ;\widehat {ADO} = 30^\circ \)
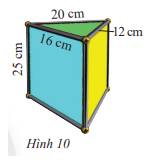



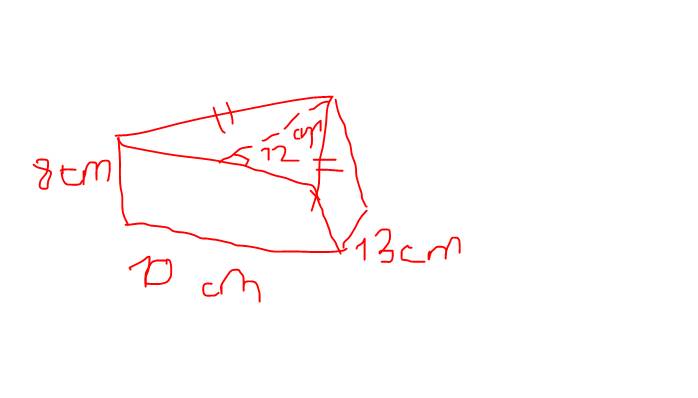
Diện tích xung quanh của chiếc hộp là:
Sxq = Cđáy . h = (20+12+16). 25 = 1200 (cm2)