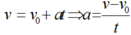Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gía tốc chất điểm:
\(v=v_0+at=0+at=at\)
\(\Rightarrow a=\dfrac{v}{t}=\dfrac{8}{4}=2\)m/s2

a) Từ công thức v 2 − v 0 2 = 2 a s ⇒ gia tốc: a = v 2 − v 0 2 2 s
Thay số ta được: a = 8 2 − 4 2 2.8 = 3 m/s2.
b) Phương trình chuyển động có dạng: x = v 0 t + 1 2 a t 2 .
Thay số ta được: x = 4 t + 1 , 5 t 2 (m).
c) Ta có: v = v 0 + a t ⇒ t = v − v 0 a = 13 − 4 3 = 3 s.
Tọa độ của chất điểm lúc đó: x = 4.3 + 1 , 5.3 2 = 25 , 5 m.

Phân tích bài toán
SAD=28m; gọi t là khoảng thời gian chất điểm đi hết đoạn đường AD
Tại B cách A 1 giây:
vB=vo + a.1=6 => vo=6-a (1)
Tại điểm C cách điểm D 1 giây:
vC=vo + a(t-1)=8 => vo + at – a=8 (2)
Giải
từ (1) và (2) => t=2a+22a+2 (3)
SAD=vot + 0,5at2=28 (4)
thay (1); (3) vào (4)
=> a=1m/s2 => t=4s;
SCD=vC.1 + 0,5a.12=8,5m.
SAD=28m; gọi t là khoảng thời gian chất điểm đi hết đoạn đường AD
Tại B cách A 1 giây:
vB=v0 + a.1=6 => v0=6-a (1)
Tại điểm C cách điểm D 1 giây:
vC=v0 + a(t-1)=8 => v0 + at – a=8 (2)
Giải
từ (1) và (2) => t=2a+22a+2 (3)
SAD=v0t + 0,5at2=28 (4)
thay (1); (3) vào (4)
=> a=1m/s2 => t=4s;
SCD=vC.1 + 0,5a.12=8,5m.

theo đề bài ta có x1=-5+5t+0,2t2
a)x=x0+v0.t+a.t2\(\Rightarrow\)\(\left\{{}\begin{matrix}a=0,4\\v_0=5\\x_0=-5\end{matrix}\right.\) (m;s)
quãng đường mà chất điểm đi được sau 5s đầu
s=v0.t+a.t2.0,5=30m
c)hai chất điểm gặp nhau x1=x2\(\Leftrightarrow\)\(-5+5t+0,2t^2=10+2t+0,1t^2\)
\(\Rightarrow\)\(\left[{}\begin{matrix}t=-15-5\sqrt{15}\left(l\right)\\t=-15+5\sqrt{15}\left(n\right)\end{matrix}\right.\)
vậy sau \(-15+5\sqrt{15}\)s hai chất điểm gặp nhau
vị trí gặp nhau x1=x2\(\approx\)20,63m

đề sai ở chỗ x=10
bỏ chỗ t=0 thì x=10 đi
còn t=5 thì x=10
phương trình có dạng
\(x=v_0.t+\frac{1}{2}.a.t^2=10\)
\(\Leftrightarrow x=5v_0+6,25=10\)
\(\Rightarrow v_0=\)0,75m/s
phương trình có dạng
\(x=x_0+v_0.t+\frac{1}{2}.a.t^2=0,75t+0,1t^2\)