Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

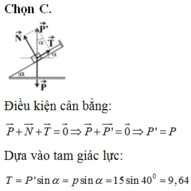
Chọn C.
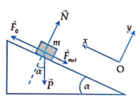
+ Khi vật trượt đều lên mặt phẳng nghiêng:
![]()
Chiếu lên phương mặt phẳng nghiêng và vuông góc với mặt phẳng nghiêng:
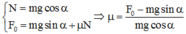
+ Khi vật trượt đều trên mặt ngang:
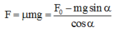

Chọn C.
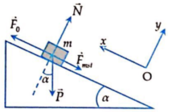
+ Khi vật trượt đều lên mặt phẳng nghiêng:
F 0 ⇀ + P ⇀ + N ⇀ + F m s ⇀ = 0 ⇀
Chiếu lên phương mặt phẳng nghiêng và vuông góc với mặt phẳng nghiêng:
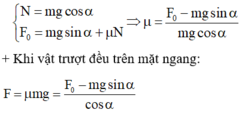

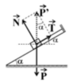
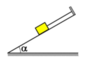
Chọn hệ trục tọa độ Oxy như hình vẽ. Gọi \(\overrightarrow{F_k}\) là lực kéo tác dụng lên sợi dây, \(\overrightarrow{P}\) và \(\overrightarrow{N}\) lần lượt là trọng lực tác dụng lên vật. Ta phân tích \(\overrightarrow{F_k}\) thành 2 lực \(\overrightarrow{F_{k_x}}\) và \(\overrightarrow{F_{k_y}}\) trên các trục Ox, Oy.
a) Công của lực kéo là \(A_k=F_k.s.cos\left(\overrightarrow{F_k},\overrightarrow{s}\right)=100.20.cos45^o=1000\sqrt{2}\left(J\right)\)
b) Gọi \(\overrightarrow{F_{ms}}\) là lực ma sát tác dụng lên vật. Chọn chiều dương là chiều chuyển động của vật
Áp dụng định luật II Newton:
\(\overrightarrow{F_k}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\) (1)
Chiếu (1) lên Oy: \(N=P-F_{k_y}=400-F_k.sin45^o=400-175\sqrt{2}\left(N\right)\)
Do đề bài không nói gì về loại chuyển động của vật nên mình sẽ xem đây là chuyển động nhanh dần đều nhé. Khi đó, ta sẽ có \(s=\dfrac{1}{2}at^2\Rightarrow20=\dfrac{1}{2}a.180^2\) \(\Rightarrow a=\dfrac{1}{810}\left(m/s^2\right)\).
Chiếu (1) lên Ox, ta được \(F_{k_x}-F_{ms}=m.a\Rightarrow F_{ms}=F_{k_x}-m.a=350.cos45^o-400.\dfrac{1}{180}\)\(=170\sqrt{2}-\dfrac{20}{9}\) (N)
\(\Rightarrow A_{ms}=-\left(170\sqrt{2}-\dfrac{20}{9}\right).20\approx-4763,88\left(J\right)\)

Công kéo vật:
\(A=F\cdot s\cdot cos\alpha=150\cdot15\cdot cos45^o=1590,99J\)
Công suất thực hiện:
\(P=\dfrac{A}{t}=F\cdot v=150\cdot1,5=225W\)

để xe chuyển động đều (a=0)
\(\overrightarrow{F_k}+\overrightarrow{P}+\overrightarrow{N}=0\)
chiếu lên trục Ox song song với mặt phằng
Fk-sin\(\alpha\).P=0
\(\Rightarrow\)Fk=150N
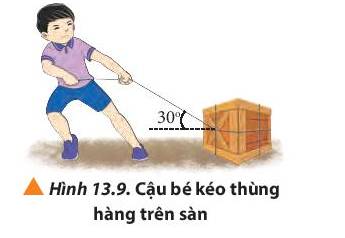
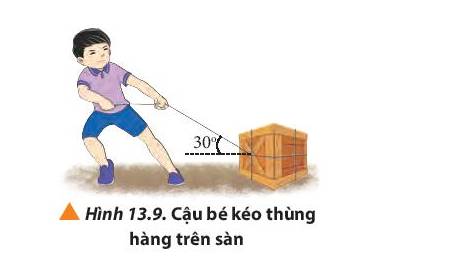

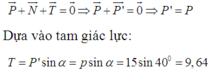
Ta có F = 12 N, α = 300
Độ lớn lực thành phần:
+ Fx = F.cosα = 12.cos300 = \(6\sqrt 3 \)(N).
+ Fy = F.sinα = 12.sin300 = 6 (N).