Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có BC < BD mà C, D nằm cùng phía so với B ⇒ C nằm giữa B và D.


Trong tam giác ACD có góc ACD là góc tù .
Mà AD là cạnh đối diện với góc ACD.
⇒ AD là cạnh lớn nhất trong tam giác ACD (cạnh đối diện với góc tù là cạnh lớn nhất trong tam giác).
nên AD > AC hay AC < AD
Vậy Nếu : BC < BD thì AC < AD.

Xets t/g ABC cân tại A
=> \(\widehat{ABC}=\dfrac{180^o-\widehat{BAC}}{2}\) (t/c) (1)Xét t/g AED có AD = AE=> t/g ADE cân tại A
=> \(\widehat{AED}=\dfrac{180^o-\widehat{BAC}}{2}\) (t/c) (2)Từ (1) ; (2)
=> \(\widehat{ABC}=\widehat{AED}\)
Mà 2 góc này ở vị trí đồng vị
=> ED // BC

a) Xét tam giác ABE và tam giác ADC:
AE=AC(theo gt tam giác ABC cân )
góc A chung
AE=AD(theo gt)
=> Tam giác ABE=tam giác ADC(c.g.c)
nên BE=CD(dpcm)
b) Vì tam giác ABE=tam giác ACD nên góc ABE=góc ACD( 2 góc tương ứng)
c) Xét Tam giác DKB và tam giác EKC
góc DKB=góc EKC(đối đỉnh)
AB=AC(tam giác ABC cân) mà AD=AE (gt) =>DB=EC
góc DBK= góc ECK
=>tam giác DKB=tam giác EKC(g.c.g)
=>KB=KC(2 cạnh tương ứng)
=>tam giác KBC là tam giác cân .
a) Xét \(\Delta\) BAE và \(\Delta\) CAD có:
AB = AC ( \(\Delta\) ABC cân tại A )
BAE = CAD ( chung góc A )
AD = AE ( giả thiết )
.=> \(\Delta\) BAE = \(\Delta\) CAD ( c . g . c ) (1)
=> BE = CD ( 2 cạnh tương ứng )
Vậy BE = CD ( đpcm)
b) Ta có: \(\Delta\) BAE = \(\Delta\) CAD ( chứng minh (1) )
=> ABE = ACD ( 2 góc tương ứng )
Vậy ABE = ACE ( đpcm )
c) Ta có: \(\Delta\) ABC cân tại A ( giả thiết )
=> ABC = ACB ( tính chất tam giác cân )
hay DBC = ECB (2)
Xét \(\Delta\) DBC và \(\Delta\) ECB có:
CD = BE ( chứng minh a)
DBC = ECB ( chứng minh (2) )
BC là cạnh chung
=> \(\Delta\) DBC = \(\Delta\) ECB ( c . g . c )
=> DCB = EBC ( 2 góc tương ứng )
hay KCB = KBC
Xét \(\Delta\) KBC có: KCB = KBC
=> \(\Delta\) KBC cân tại K
Vậy \(\Delta\) KBC cân tại K
Chuk bn hk tốt ! ![]()

Hình bạn tự vẽ.
Xét \(\Delta ABC\)cân tại A ta có:
\(\widehat{DAC}=180^o-2\widehat{ACD}\)
\(\widehat{DAC}=180^o-2\cdot31^o=118^o\)
Mà \(\widehat{DAC}=\widehat{ABD}+\widehat{ADB}\)( góc ngoài tại đỉnh A của \(\Delta ABD\))
Nên \(118^o=88^o+\widehat{ADB}\)
\(\Rightarrow\)\(\widehat{ADB}=118^o-88^o=30^o\)
Mặt khác \(\widehat{ADB}=\widehat{DEC}\)( 2 góc so le trong và BD // EC )
\(\Rightarrow\)\(\widehat{DEC}=30^o\)
Ta có:
\(\widehat{ACE}=\widehat{ABD}\)( 2 góc so le trong và BD // EC )
\(\widehat{ABD}=88^o\left(gt\right)\)
\(\Rightarrow\)\(\widehat{ACE}=88^o\)
Mà \(\widehat{DCE}=\widehat{ACD}+\widehat{ACE}\)
Nên \(\widehat{DCE}=31^o+88^o=119^o\)
Ta có:
\(\widehat{ACD}=\widehat{ADC}\)( \(\Delta ACD\)cân tại A)
\(\widehat{ACD}=31^o\)
\(\Rightarrow\)\(\widehat{ADC}=31^o\)
Xét \(\Delta ECD\)ta có:
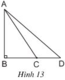
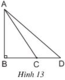
\(\widehat{DCE}>\widehat{EDC}>\widehat{DEC}\left(119^o>31^o>30^o\right)\)
\(\Rightarrow\)\(ED>EC>CD\)( Quan hệ cạnh góc đối diện trong tam giác )
Vậy cạnh \(DE\)lớn nhất trong \(\Delta CDE\)
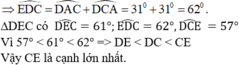
Lời giải
a)Từ giả thiết đã cho, ta có : góc ACD = góc B + góc BAC ( tính chất góc ngoài tam giác)
mà góc B=90 độ
suy ra góc ACD > góc B hay góc ACD > 90 độ
Từ trên ta có thể suy ra góc ACD là góc tù ( dựa vào tính chất góc tù )
b) Trong tam giác ACD, có : góc ACD tù tức là góc ACD > 90 độ suy ra AC > AD ( quan hệ giữa góc và cạnh đối diện trong tam giác ) hoặc (nhận xét về tính chất góc tù) hay ( cạnh đối diện với góc tù bao giờ cũng lớn hơn cạnh còn lại )