Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp giải: Áp dụng nguyên lý bù trừ trong bài toán xác suất
Lời giải:
Ta tính xác suất để xảy ra không một lá thư nào đúng địa chỉ.
Mỗi phong bì có 4 cách bỏ thư vào nên có tất cả 4! cách bỏ thư.
Gọi U là tập hợp các cách bò thư và A m là tính chất lá thư thứ m bỏ đúng địa chỉ.
Khi đó, theo công thức về nguyên lý bù trừ, ta có N ¯ = 4 ! − N 1 + N 2 − ... + − 1 4 N 4
Trong đó N m 1 ≤ m ≤ 4 là số tất cả các cách bỏ thư sao cho có m lá thư đúng địa chỉ.
Nhận xét rằng, N m là tổng theo mọi cách lấy m lá thư từ 4 lá, với mỗi cách lấy m lá thư, có 4 − m ! cách bỏ m lá thư này đúng địa chỉ, ta nhận được: N m = C 4 m . 4 − m ! = 4 ! k ! và
N ¯ = 4 ! 1 − 1 1 ! + 1 2 ! − ... + − 1 n . 1 4 !
Suy ra xác suất cần tìm cho việc không lá thư nào đúng địa chỉ là P ¯ = 1 − 1 1 ! + 1 2 ! − ... + − 1 4 . 1 4 !
Vậy xác suất để có ít nhất 1 lá thư bỏ đúng phong bì của nó là P = 1 − P ¯ = 5 8

Đáp án B
Ta xét bài toán tổng quát n tem thư được dán vào n bì thư sao cho có ít nhất 1 bì thư được dán vào tem thư có số trùng với số của bì thư đó
Đánh số các tem thư là T 1 , T 2 ,.., T n và các bì thư B 1 , B 2 ,…, B n . Bài toán được giải quyết bằng nguyên lý phần bù. Lấy hoán vị n phần tử trừ đi trường hợp xếp mà không có tem thư nào được dán cùng số với bì thư.
+ Để giải quyết bài toán không có tem thư nào được dán cùng số với bì thư. Ta xây dựng dãy số f(n) như sau:
Công việc dán n tem thư vào n bì thư sao cho không có bì thư nào được dán vào tem thư có số trùng với số của bì thư đó. Công việc này gồm có 2 bước sau
- Bước 1: dán tem T1 lên 1 bì thư Bj khác B1, có n – 1 cách
- Bước 2: Dán tem thư Tj vào bì thư nào đó, có 2 trường hợp xảy ra như sau:
+ TH1: Tem thư Tj được dán vào bì thư B1. Khi đó còn lại n – 2 tem (khác T1 và Tj) là T2,…,Tj-1, Tj+1,…,Tn phải dán vào n – 2 bì thư (khác B1 và Bj). Quy trình được lặp lại giống như trên. Nên TH này có số cách dán bằng f(n-2)
+ TH2: tem thư Tj không được dán vào bì thư B1
Khi đó các tem là T2,…,Tj-1, Tj, Tj+1,…,Tn sẽ được đem dán vào các bì B1, B2,…,Bj-1, Bj+1,…,Bn (mà tem thư Tj không được dán vào bì thư B1). Thì Tj lúc này bản chất giống như T1, ta đánh số lại Tj º T1. Nghĩa là n – 1 tem T2, …, Tj-1, T1, Tj+1,…,Tn sẽ được đem dán vào n – 1 bì B1, B2,…,Bj-1,Bj+1,…,Bn với việc đánh số giống nhau. Công việc này lại được lập lại như từ ban đầu.
Nên TH này có số cách dán bằng f (n-1)
+ Ta xét dãy u n = f n như sau
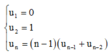
Như vậy kết quả của bài toán: n tem thư được dán vào n bì thư sao cho có ít nhất 1 bì thư được dán vào tem thư có số trùng với số của bì thư đó sẽ là P n - u n
Áp dụng với n = 8, ta được kết quả là 8!-14833=25487.

Xét các dãy số x 1 ; x 2 ; x 3 , trong đó x 1 ; x 2 ; x 3 là một hoán vị của ba số 1,2,3 (ở đây x i = i , tức là lá thư i đã bỏ đúng địa chỉ).
Gọi Ω là tập hợp tất cả các khả năng bỏ 3 lá thư vào 3 phong bì. Khi đó Ω = 3 ! = 6 .
Gọi A là biến cố: “Có ít nhât 1 lá thư bỏ đúng phong bì”. Các khả năng thuận lợi của A là ( 1;2;3 ); ( 1;3;2 ); ( 3;2;1 ); ( 2;1;3 ). Do vậy Ω A = 4 .
Từ đó P ( A ) = Ω A Ω = 4 6 = 2 3
Đáp án cần chọn là A

goi so ban trong lop hoc la b
so hoc sinh cua 1 lop khi xep 4 ban 1 ban thi thua2 bạn la:4.b+2
so hoc sinh cua 1 lop khu xep 5 ban 1 ban thi thua 2 bàn la:5.(b-2)
vay ta co:4.b+2=5(b-2)
tu dó suy ra:b=12
suy ra so ban lop 4a la:
4.12+2=50(ban)
dap so:50 ban
Số hs của lớp 4A chỉ có thể là số có 2 chữ số. Số hs lớp đó chia hết cho 5 và chia cho 4 dư 2 và số đó là số có tận cùng là chữ số 0. Có các số sau: 10, 30, 50, 70, 90
– Nếu số hs lớp đó là 10 em thì số bàn cần để xếp hs ngồi theo nhóm 4 bạn và xếp 2 bạn còn lại vào 2 bàn đầu là 2 bàn. Nếu ngồi 5 thì số bàn đó là đủ chứ k thừa ra 2 bàn như đề bài nên lớp 4A k thể có 10hs.
– Nếu lớp 4A có 30 hs thì xếp theo bàn 4 sẽ cần số bàn là 7 bàn. Nếu ngồi 5 thì sẽ là 6 bàn, vậy chỉ dôi ra 1 bàn nên hs lớp 4A k thể là 30.
– Nếu lớp 4A có 50hs thì ngồi 4 sẽ cần số bàn là 12 bàn. Nếu ngồi 5 sẽ là 10 bàn và như vậy sẽ thừa ra 2 bàn. Như vậy số hs lớp 4A là 50 em.
– Làm tương tự như vậy thì 70, 90 loại.
Vậy số hs 4A là 50 em

1 người bán 2/3 tấm vải nhung với giá 60000 đồng 1 m . Chỗ còn lại người đó bán 65000 đồng 1 m. tiền lãi được tất cả 287000 đồng, biết giá vốn là 48000 đồng 1 m . Tính chiều dài tấm nhung

17va20