Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình trình bày cho dễ hiểu nha
\(sina-\sqrt{3}cosa\)
\(=2\cdot\left(\frac{1}{2}sina-\frac{\sqrt{3}}{2}cosa\right)\)
\(=2\cdot\left(sinacos\frac{pi}{6}-cosasin\frac{pi}{6}\right)\)
\(=2\cdot sin\left(a-\frac{pi}{6}\right)\)
Ta có\(-1\le sin\left(a-\frac{pi}{6}\right)\le1\)
\(-2\le sin\left(a-\frac{pi}{6}\right)\le2\)
Vậy Min=-2
Max=2

\(cos\alpha=\frac{1}{2}\Leftrightarrow\alpha=\frac{-\pi}{3}\)(vì \(\frac{-\pi}{2}< \alpha< 0\))
\(cot\left(\frac{\pi}{3}-\alpha\right)=cot\left(\frac{2\pi}{3}\right)=\frac{-\sqrt{3}}{3}\)

Ta thừa nhận định lý f(x) chia hết cho x-a thì f(a) =0 ( mình đang vội khỏi chứng minh nhé, nếu thắc mắc phiền bạn xem SGK 9 nha)
Thay 1 vào x, ta có
f(x) =14+12+a=0
2+a=0 suy ra a=-2



Ta có \(D=sin^2a-cosa-1=-cos^2a-cosa=-\left(cos^2a+cosa+\frac{1}{4}\right)+\frac{1}{4}\le\frac{1}{4}\)
mình đang học onl nên là rep muộn chút
Đặt \(sina=x;cosa=y\)ta có : \(x^2+y^2=1\)
Khi đó : \(-E=x^2+y^2-x-y-1=\left(x-\frac{1}{2}\right)^2+\left(y-\frac{1}{2}\right)^2-\frac{3}{2}\ge-\frac{3}{2}\)
\(< =>E\le\frac{3}{2}\)
sai thì thôi nhé


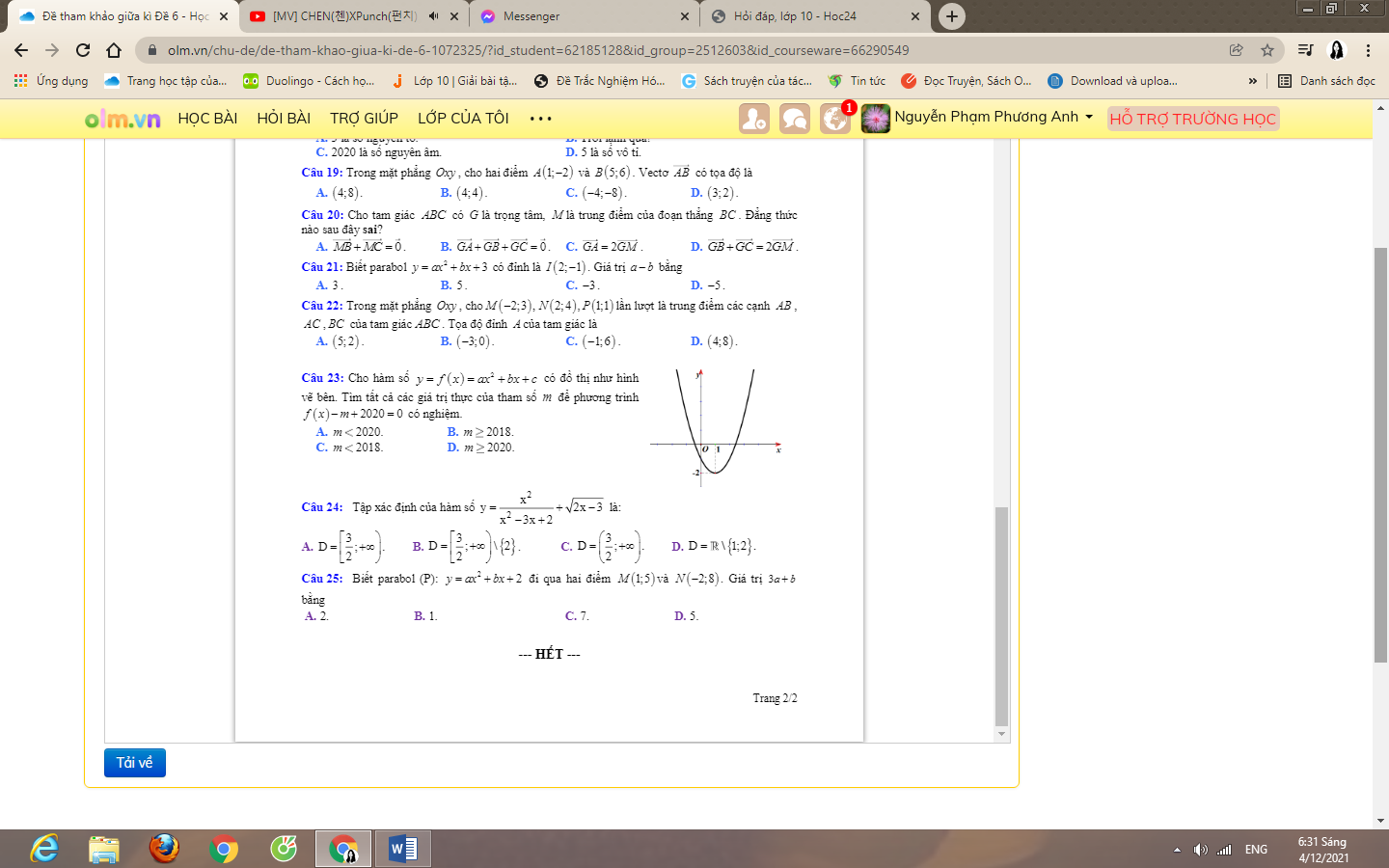










Câu 25: B