
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Một nghìn không trăm hai mươi chín phẩy bốn trăm tám mươi sáu tỷ đồng

Chọn A
Tập xác định: D = ℝ
Đạo hàm: y ' = 3 x 2 - 6 x - 9
![]()
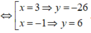
Bảng biến thiên
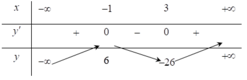
Hàm số đồng biến trên các khoảng - ∞ ; - 1 v à 3 ; + ∞
Do đó hàm số đồng biến trên khoảng 4 ; 5

Đáp án C.
Hàm số y = -x4 + 2x2 có y’ = -4x3 + 4x, y’ ≥ 0
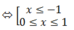
Vậy hàm số đã cho đồng biến trên (-∞; -1)

Lời giải:
$y'=\frac{2x}{\sqrt{2x^2+1}}$
$y'>0\Leftrightarrow 2x>0\Leftrightarrow x>0$ hay $x\in (0;+\infty)$
$y'< 0\Leftrightarrow 2x< 0\Leftrightarrow x\in (-\infty;0)$
Vậy hàm số đồng biến trên $(0;+\infty)$ và nghịch biến trên $(-\infty; 0)$
Đáp án A.

Chọn D.
TXĐ: D = R

Trên các khoảng ![]() y’ > 0 nên hàm số đồng biến
y’ > 0 nên hàm số đồng biến
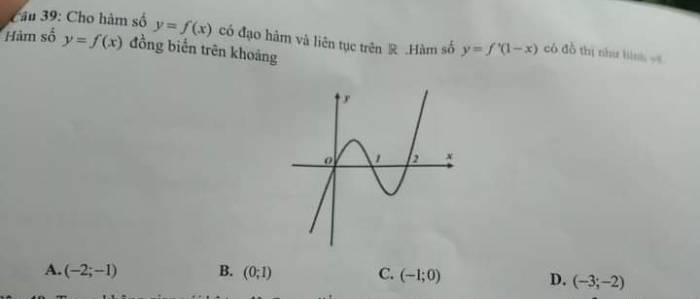
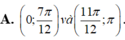
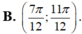
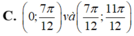
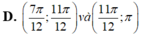

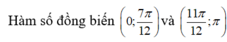
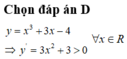
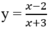
Đặt \(x=1-t\Rightarrow y=f\left(1-t\right)\Rightarrow y'=-f'\left(1-t\right)\) trái dấu với \(f'\left(1-t\right)\)
Từ đồ thị ta thấy \(f'\left(1-t\right)\) âm khi \(\left[{}\begin{matrix}t< 0\\1< t< 2\end{matrix}\right.\) hay \(y'\) dương khi \(\left[{}\begin{matrix}t< 0\\1< t< 2\end{matrix}\right.\)
Hay \(\left[{}\begin{matrix}1-x< 0\\1< 1-x< 2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x>1\\-1< x< 0\end{matrix}\right.\)