K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 1
Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x-y}{2-3}=\dfrac{3}{-1}=-3\)
\(\Rightarrow\left\{{}\begin{matrix}x=-3.2=-6\\y=-3.3=-9\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 1
Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{-18}{9}=-2\)
\(\Rightarrow\left\{{}\begin{matrix}x=-2.2=-4\\y=-2.3=-6\\z=-2.4=-8\\\end{matrix}\right.\)
20 tháng 1
nếu muốn sửa đoạn đường trong 5 ngày thì số công nhân cần dùng đến là:
\(8\cdot10:5=16\left(người\right)\)
20 tháng 3 2023
16:
a: Xét ΔDHB vuông tại H và ΔEKC vuông tại K có
BD=CE
góc B=góc C
=>ΔDHB=ΔEKC
=>DH=EK
b: Xét ΔAHD vuông tại H và ΔAKE vuông tại K có
AH=AK
HD=KE
=>ΔAHD=ΔAKE
=>AD=AE
5 tháng 1
a: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: AB=AM
=>A nằm trên đường trung trực của BM(1)
Ta có: DB=DM
=>D nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AD là đường trung trực của BM
CH
27 tháng 1
Gọi số cây trồng của ba lớp `7A,7B,7C` lần lượt là `x,y,z` (cây; `x,y,z>0`)
`-` Theo đề bài, ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\) và `x+y+z=120`
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y+z}{3+4+5}=\dfrac{120}{12}=12\)
\(\Rightarrow\\ x=3\cdot10=30\\ y=4\cdot10=40\\ z=5\cdot10=50\)
Vậy, số cây trồng được của ba lớp `7A,7B,7C` lần lượt là `30,40,50` cây.
T
12 tháng 1
a) \(\dfrac{x}{-15}=\dfrac{-60}{3}\)
\(\Rightarrow x:\left(-15\right)=-20\)
\(\Rightarrow x=-20\cdot\left(-15\right)\)
\(\Rightarrow x=300\)
b) \(\dfrac{3,5}{15}=\dfrac{-2}{x}\)
\(\Rightarrow3,5\cdot x=-2\cdot15\)
\(\Rightarrow3,5x=-30\)
\(\Rightarrow x=-30:3,5\)
\(\Rightarrow x=-\dfrac{60}{7}\)
12 tháng 1
a: \(\dfrac{x}{-15}=-\dfrac{60}{3}\)
=>\(\dfrac{x}{15}=\dfrac{60}{3}\)
=>\(\dfrac{x}{15}=20\)
=>\(x=20\cdot15=300\)
b: \(\dfrac{3.5}{15}=\dfrac{-2}{x}\)
=>\(x=\dfrac{15\cdot\left(-2\right)}{3,5}=-\dfrac{30}{3,5}=-\dfrac{60}{7}\)
12 tháng 1
a: \(\dfrac{8}{12}:\dfrac{4}{15}=\dfrac{8}{12}\cdot\dfrac{15}{4}=\dfrac{120}{48}=\dfrac{5}{2}\)
b: \(\dfrac{0.75}{2.5}=\dfrac{75}{250}=\dfrac{3}{10}\)
12 tháng 1
\(\left(-10\right)\cdot20=\left(-25\right)\cdot8\)
=>\(\dfrac{-10}{-25}=\dfrac{8}{20};\dfrac{-10}{8}=\dfrac{-25}{20};\dfrac{-25}{-10}=\dfrac{20}{8};\dfrac{8}{-10}=\dfrac{20}{-25}\)
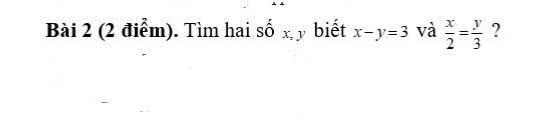
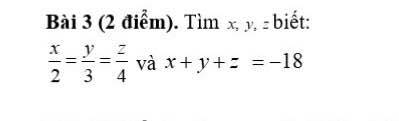
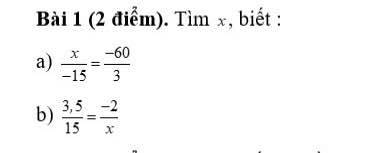
Do \(EF>DF>DE\)
\(\Rightarrow\widehat{D}>\widehat{E}>\widehat{F}\) (góc đối diện với cạnh lớn hơn thì lớn hơn)