K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 2 2022
Xét ΔPMN có PQ là đường phân giác
nên MQ/MP=NQ/NP
hay MQ/6,2=NQ/8,7
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{MQ}{6.2}=\dfrac{NQ}{8.7}=\dfrac{MQ+NQ}{6.2+8.7}=\dfrac{12.5}{14.9}=\dfrac{125}{149}\)
=>MQ=775/149(cm); NQ=2175/298(cm)
5 tháng 3 2022
a, Xét tam giác AMN và tam giác ABC có
^A _ chung
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{2,5}{7,5}=\dfrac{3}{9}=\dfrac{1}{3}\)
Vậy tam giác AMN ~ tam giác ABC (c.g.c)
b, Ta có tỉ số đồng dạng : \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\Rightarrow MN=\dfrac{AM.BC}{AB}=4cm\)
5 tháng 3 2022
a.Ta có:
\(\dfrac{AM}{AB}=\dfrac{2,5}{7,5}=\dfrac{1}{3};\dfrac{AN}{AC}=\dfrac{3}{9}=\dfrac{1}{3}\)
\(\Rightarrow\)MN//BC ( Ta-lét đảo )
=> Tam giác AMN đồng dạng tam giác ABC
b. Ta có: MN//BC ( cmt )
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MN}{BC}\)
\(\Leftrightarrow\dfrac{1}{3}=\dfrac{MN}{12}\)
\(\Leftrightarrow3MN=12\)
\(\Leftrightarrow MN=4cm\)
8 tháng 2 2022
-Hình vẽ:
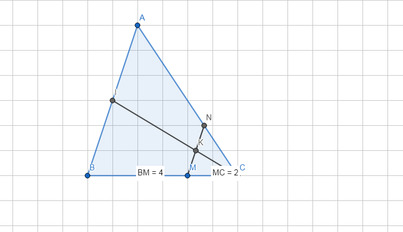
a) Ta có: \(\dfrac{CM}{BM}=\dfrac{1}{2}\Rightarrow\dfrac{BM}{CM}=2\).
-Xét △ABC có: \(\dfrac{BM}{CM}=\dfrac{AN}{NC}=2\) .
\(\Rightarrow MN\)//\(AB\) (định lí Ta-let đảo).
b) -Xét △BCI có: MK//BI (cmt).
\(\Rightarrow\dfrac{MK}{BI}=\dfrac{CK}{CI}\) (định lí Ta-let) (1).
-Xét △ACI có: NK//AI (cmt).
\(\Rightarrow\dfrac{NK}{AI}=\dfrac{CK}{CI}\) (định lí Ta-let) (2).
-Từ (1) và (2) suy ra: \(\dfrac{MK}{BI}=\dfrac{NK}{AI}\)
Mà \(BI=AI\) (I là trung điểm AB).
\(\Rightarrow MK=NK\) hay K là trung điểm MN.
22 tháng 1 2022
a: AE=1/3x6=2(cm)
b: AE/AB=AF/AC
c: Xét ΔABC có EF//BC
nên AE/AB=AF/AC
=>AF/7=1/3
hay AF=7/3(cm)
15 tháng 1 2022
a: \(S_{ABCD}=\dfrac{AD\cdot DC}{2}=\dfrac{12\cdot16}{2}=12\cdot8=96\left(cm^2\right)\)
b: MD=6cm
DO=5cm
4 tháng 1 2022
a: Xét tứ giác BDCN có
M là trung điểm của BC
M là trung điểm của DN
Do đó: BDCN là hình bình hành
b: Xét tứ giác ANDB có
DB//AN
DB=AN
Do đó: ANDB là hình bình hành
mà \(\widehat{NAB}=90^0\)
nên ANDB là hình chữ nhật
Suy ra: AD=BN
L
4 tháng 1 2022
a)
Vì D đối xứng N qua M (gt)
=> M là trung điểm của DM (đn)
Xét tứ giác BDCN có
M là trung điểm BC (gt)
M là trung điểm DM (cmt)
=> Tứ giác BDCN là hbh (dhnb hbh)
b)
Vì BDCN là hbh( cmt)
=> BD//NC
=> BD//AN (1) và BD=NC
mà NC=AN (N là trung điểm AC)
=> BD=NC (bắc cầu) (2)
Mà BAC=90 (gt) (3)
Từ (1) và (2), (3)=> BDNA hcn (dhnb hcn)
=> AD=BN (t/c đường chéo hcn)
Xét tam giác ACE có
N là trung điểm AC (gt)
FN//EC (BN//DC)
=> F là trung điểm của AE ( đtb)
mà N là trung điểm của AC (gt)
=> FN là đtb của tam giác AEC ( đn)
=> FN= 1/2 EC (1)
Xét tam giác FNM=tam giác EMD (cgc)
=> DE=FN ( 2 góc t/ư)(2)
Từ (1) và (2) => DE=1/2 EC ( bc)
a: Ta có: BEDC là hình bình hành
nên BE//DC và BE=DC
=>BE=AB
Ta có: BE//DC
AB//DC
mà AB và BE cắt nhau tại B
nên A,B,E thẳng hàng
mà BA=BE
nên B là trung điểm của AE
b: Ta có: BDCE là hình bình hành
nên BD//CE và BD=CE(1)
Ta có: BDFC là hình bình hành
nên BD//FC và BD=FC(2)
Từ (1) và (2) suy ra CE=FC
Ta có: BD//CE
BD//FC
mà FC,CE có điểm chung là C
nên F,C,E thẳng hàng
mà CE=CF
nên C là trung điểm của FE