K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 1 2023
a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
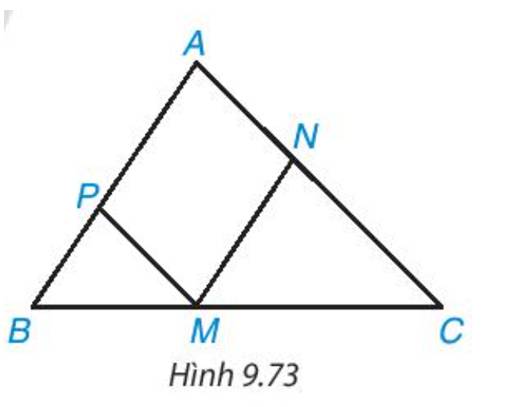
- ΔCNM ~ ΔCAB (vì MN // AB) (1)
- ΔMPB ~ ΔCAB (vì MP // AC) (2)
- Từ (1) và (2) => ΔCNM ~ ΔMPB
HQ
Hà Quang Minh
Giáo viên
11 tháng 1 2024
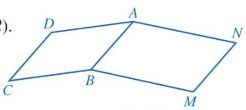
a, Do ABCD là hình bình hành: AB = CD.
Do ABMN là hình bình hành: AB = MN
Suy ra: CD = MN = AB
b, Do ABCD là hình bình hành \( \Rightarrow \widehat {BCD} = \widehat {DAB}\)
Do ABMN là hình bình hành \( \Rightarrow \widehat {BMN} = \widehat {NAB}\)
\(\widehat {BCD} + \widehat {BMN} = \widehat {DAB} + \widehat {NAB} = \widehat {DAN}\)
HQ
Hà Quang Minh
Giáo viên
11 tháng 1 2024
Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)
TM
18 tháng 7 2023
1.
\(A=\dfrac{x\left(x^2+x-6\right)}{x\left(x^2-4\right)}=\dfrac{\left(x^2-4\right)+x-2}{x^2-4}=\dfrac{\left(x-2\right)\left(x+2\right)+x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x-2\right)\left(x+2+1\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+3}{x+2}\)
thay x = 98 ta được: \(A=\dfrac{101}{100}\)
2. (đkxd \(x\ne\pm1\))
\(B=\dfrac{x-1}{x+1}+\dfrac{x+1}{x-1}+\dfrac{5x}{1-x^2}=\dfrac{\left(x-1\right)^2}{\left(x+1\right)\left(x-1\right)}+\dfrac{\left(x+1\right)^2}{\left(x+1\right)\left(x-1\right)}-\dfrac{5x}{\left(x+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2+\left(x+1\right)^2-5x}{x^2-1}=\dfrac{x^2-2x+1+x^2+2x+1-5x}{x^2-1}=\dfrac{2x^2-5x+2}{x^2-1}=\dfrac{2x^2-4x-x+2}{x^2-1}=\dfrac{2x\left(x-2\right)-\left(x-2\right)}{x^2-1}=\dfrac{\left(x-2\right)\left(2x-1\right)}{x^2-1}\)để B bằng 0 thì: \(\left(x-2\right)\left(2x-1\right)=0\left(x^2-1\ge0\forall x\ne\pm1\right)\Leftrightarrow\left[{}\begin{matrix}x-2=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=\dfrac{1}{2}\left(tm\right)\end{matrix}\right.\)
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
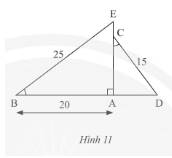
Xét \(\Delta ABE\) và \(\Delta ACD\) có:
\(\widehat {EBA} = \widehat {ACD}\) (giả thuyết)
\(\widehat {BAE} = \widehat {CAD} = 90^\circ \)
Do đó, \(\Delta ABE\backsim\Delta ACD\) (g.g)
Vì \(\Delta ABE\backsim\Delta ACD\) nên \(\frac{{AB}}{{AC}} = \frac{{EB}}{{CD}}\) (các cặp cạnh tương ứng)
Thay số, \(\frac{{20}}{{AC}} = \frac{{25}}{{15}} \Rightarrow AC = \frac{{20.15}}{{25}} = 12\)cm.
Áp dụng định lí Py – ta – go cho \(\Delta ABE\) vuông tại \(A\) ta có:
\(B{E^2} = A{E^2} + A{B^2} \Leftrightarrow A{E^2} = B{E^2} - A{B^2} = {25^2} - {20^2} = 225 \Rightarrow AE = \sqrt {225} = 15\)cm.
Độ dài \(CE\) là:
15 – 12 = 3cm
Vậy \(CE = 3cm.\)
Bài 1. (a) Điều kiện: \(x\ne\pm1\).
Ta có: \(A=\left(\dfrac{x-2}{x-1}-\dfrac{x+3}{x+1}+\dfrac{3}{x-1}\right):\left(1-\dfrac{x+3}{x+1}\right)\)
\(=\left(\dfrac{x-2+3}{x-1}-\dfrac{x+3}{x+1}\right):\dfrac{x+1-\left(x+3\right)}{x+1}\)
\(=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right):\dfrac{x+1-x-3}{x+1}\)
\(=\dfrac{\left(x+1\right)^2-\left(x+3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}:\dfrac{-2}{x+1}\)
\(=\dfrac{x^2+2x+1-x^2-2x+3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{-2}\)
\(=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{-2}=\dfrac{2}{1-x}\)
Vậy: \(A=\dfrac{2}{1-x}\)
(b) \(A=3\Leftrightarrow\dfrac{2}{1-x}=3\)
\(\Rightarrow1-x=\dfrac{2}{3}\Leftrightarrow x=\dfrac{1}{3}\left(TM\right)\)
Vậy: \(x=\dfrac{1}{3}\)
Bài 2. (a) Phương trình tương đương với:
\(\dfrac{3\left(3x-2\right)}{12}+\dfrac{6\left(x+3\right)}{12}=\dfrac{4\left(x-1\right)}{12}+\dfrac{x+1}{12}\)
\(\Rightarrow3\left(3x-2\right)+6\left(x+3\right)=4\left(x-1\right)+x+1\)
\(\Leftrightarrow9x-6+6x+18=4x-4+x+1\)
\(\Leftrightarrow10x=-15\Leftrightarrow x=-\dfrac{3}{2}\)
Vậy: Phương trình có tập nghiệm \(S=\left\{-\dfrac{3}{2}\right\}\).
(b) Điều kiện: \(x\ne\pm1\). Phương trình tương đương với:
\(\dfrac{2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{2\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{2x^2+2}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow2\left(x+1\right)+2\left(x-1\right)=2x^2+2\)
\(\Leftrightarrow2x+2+2x-2=2x^2+2\)
\(\Leftrightarrow2x^2-4x+2=0\Leftrightarrow2\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow2\left(x-1\right)^2=0\Rightarrow x-1=0\Leftrightarrow x=1\left(KTM\right)\)
Vậy: Phương trình có tập nghiệm \(S=\varnothing\)