K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
XO
3 tháng 10 2020
Ta có : \(\hept{\begin{cases}\left|x^2+x-2\right|\ge0\forall x\\\left|x^2-1\right|\ge0\forall x\end{cases}}\Rightarrow\left|x^2+x-2\right|+\left|x^2-1\right|\ge0\forall x\)
Đẳng thức |x2 + x - 2| + |x2 - 1| = 0 xảy ra
<=> \(\hept{\begin{cases}x^2+x-2=0\\x^2-1=0\end{cases}}\Rightarrow\hept{\begin{cases}x^2+2x-x-2=0\\x^2=1\end{cases}}\Rightarrow\hept{\begin{cases}\left(x+2\right)\left(x-1\right)=0\\x^2=1\end{cases}}\)
+) Nếu : (x + 2)(x - 1) = 0
=> \(\orbr{\begin{cases}x+2=0\\x-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-2\\x=1\end{cases}}\)
+) Nếu x2 = 1
=> \(\orbr{\begin{cases}x=1\\x=-1\end{cases}}\)
Vậy x = 1
8 tháng 12 2021
\(a,B=4\sqrt{x+1}-3\sqrt{x+1}+\sqrt{x+1}+2\sqrt{x+1}=4\sqrt{x+1}\\ b,B=8\Leftrightarrow4\sqrt{x+1}=8\\ \Leftrightarrow\sqrt{x+1}=2\\ \Leftrightarrow x+1=4\\ \Leftrightarrow x=3\left(tm\right)\)
NQ
0
31 tháng 7 2023
1:
a: \(P=B:A\)
\(=\dfrac{3\sqrt{x}-3-2\sqrt{x}+4+\sqrt{x}+2}{x-4}:\dfrac{4\sqrt{x}-1}{x-4}\)
\(=\dfrac{2\sqrt{x}+3}{x-4}\cdot\dfrac{x-4}{4\sqrt{x}-1}=\dfrac{2\sqrt{x}+3}{4\sqrt{x}-1}\)
b: Để P nguyên thì \(2\sqrt{x}+3⋮4\sqrt{x}-1\)
=>\(4\sqrt{x}+6⋮4\sqrt{x}-1\)
=>\(4\sqrt{x}-1+7⋮4\sqrt{x}-1\)
=>4căn x-1 thuộc {1;-1;7;-7}
=>căn x thuộc {1/2;0;2}
mà x nguyên và x>=0 và x<>4
nên x thuộc {0}
Y
11 tháng 7 2023
\(a,A=\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{\left(2\sqrt{2}-\sqrt{5}\right)^2}\\ =\left|2-\sqrt{5}\right|+\left|2\sqrt{2}-\sqrt{5}\right|\\ =\sqrt{5}-2+2\sqrt{2}-5\\ =2\sqrt{2}-2\)
\(b,B=\sqrt{\left(\sqrt{7}-2\sqrt{2}\right)^2}+\sqrt{\left(3-2\sqrt{2}\right)^2}\\ =\left|\sqrt{7}-2\sqrt{2}\right|+\left|3-2\sqrt{2}\right|\\ =2\sqrt{2}-\sqrt{7}+3-2\sqrt{2}\\ =-\sqrt{7}+3\)
NH
11 tháng 7 2023
a)
\(A=\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{\left(2\sqrt{2}-\sqrt{5}\right)^2}\\ =\left|2-\sqrt{5}\right|+\left|2\sqrt{2}-\sqrt{5}\right|\)
\(=\sqrt{5}-2+2\sqrt{2}-\sqrt{5}\) (vì \(2-\sqrt{5}< 0;2\sqrt{2}-\sqrt{5}>0\) )
\(=2\sqrt{2}-2\)
b)
\(B=\sqrt{\left(\sqrt{7}-2\sqrt{2}\right)^2}+\sqrt{\left(3-2\sqrt{2}\right)^2}\\ =\left|\sqrt{7}-2\sqrt{2}\right|+\left|3-2\sqrt{2}\right|\)
\(=2\sqrt{2}-\sqrt{7}+3-2\sqrt{2}\) (vì \(\sqrt{7}-2\sqrt{2}< 0;3-2\sqrt{2}>0\) )
\(=3-\sqrt{7}\)
29 tháng 8 2023
\(P=\dfrac{Q}{R}=\dfrac{3\sqrt{x}-1}{x-4}:\dfrac{2}{\sqrt{x}-2}\)
\(=\dfrac{3\sqrt{x}-1}{x-4}\cdot\dfrac{\sqrt{x}-2}{2}=\dfrac{3\sqrt{x}-1}{2\sqrt{x}+4}\)
P là số nguyên
=>\(3\sqrt{x}-1⋮2\sqrt{x}+4\)
=>\(6\sqrt{x}-2⋮2\sqrt{x}+4\)
=>\(6\sqrt{x}+12-14⋮2\sqrt{x}+4\)
=>\(2\sqrt{x}+4\inƯ\left(-14\right)\)
mà 2*căn x+4>=4
nên \(2\sqrt{x}+4\in\left\{7;14\right\}\)
=>\(2\sqrt{x}\in\left\{3;10\right\}\)
=>\(x\in\left\{\dfrac{9}{4};25\right\}\)
H9
HT.Phong (9A5)
CTVHS
30 tháng 8 2023
Ta có:
\(\dfrac{Q}{R}\) là:
\(\dfrac{3\sqrt{x}-1}{x-4}:\dfrac{2}{\sqrt{x}-2}\) (ĐK: \(x\ge0;x\ne4\))
\(=\dfrac{3\sqrt{x}-1}{\left(\sqrt{x}\right)^2-2^2}:\dfrac{2}{\sqrt{x}-2}\)
\(=\dfrac{3\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{\left(3\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{2\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}-1}{2\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\sqrt{x}-1}{2\sqrt{x}+4}\)
Để giá trị của biểu thức \(\dfrac{Q}{R}\) nguyên thì
\(3\sqrt{x}-1\) chia hết cho \(2\sqrt{x}+4\)
⇒ \(2\left(3\sqrt{x}-1\right)\) chia hết cho \(2\sqrt{x}+4\)
⇒ \(6\sqrt{x}-2\) chia hết cho \(2\sqrt{x}+4\)
⇒ \(6\sqrt{x}+12-14\) chia hết cho \(2\sqrt{x}+4\)
⇒ \(3\left(2\sqrt{x}+4\right)-14\) chia hết cho \(2\sqrt{x}+4\)
⇒ - 14 chia hết cho \(2\sqrt{x}+4\)
Mà: Ư(-14)\(=\left\{1;-1;2;-2;7;-7;14;-14\right\}\)
ĐK: \(2\sqrt{x}+4\ge4\)
\(\Rightarrow2\sqrt{x}+4\in\left\{7;14\right\}\)
\(\Rightarrow x\in\left\{\dfrac{9}{4};25\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1
1.
\(\Delta'=\left(m+1\right)^2-\left(m^2+3m-7\right)=-m+8\)
Phương trình đã cho vô nghiệm khi và chỉ khi \(\Delta'< 0\)
\(\Rightarrow-m+8< 0\)
\(\Rightarrow m>8\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1
2.
Do pt có 1 nghiệm bằng 2, thay \(x=2\) vào pt ta được:
\(2^2-2\left(m-1\right)-m=0\)
\(\Rightarrow6-3m=0\Rightarrow m=2\)
Khi đó nghiệm còn lại (tính theo định lý Viet là):
\(x_1x_2=-m\Rightarrow x_2=\dfrac{-m}{x_1}=\dfrac{-2}{2}=-1\)
PK
21 tháng 1
x^2-(m-1)x-m=0 (*)
Ta có x=2 thế vào pt(*),ta có:
2^2-(m-1).2-m=0
<=> 4-2m+2-m=0
<=> -3m=-6
<=> m=2
Thế m=2 vào lại pt(*),ta lại có:
x^2-(2-1)x-2=0
<=> x^2-x-2=0
<=> x^2-2x+x-2=0
<=> (x^2-2x)+(x-2)=0
<=>x(x-2)+(x-2)=0
<=> (x-2)(x+1)=0
<=> x-2=0 hoặc x+1=0
<=>x=2 hoặc x=-1
Vậy S={−1;2}
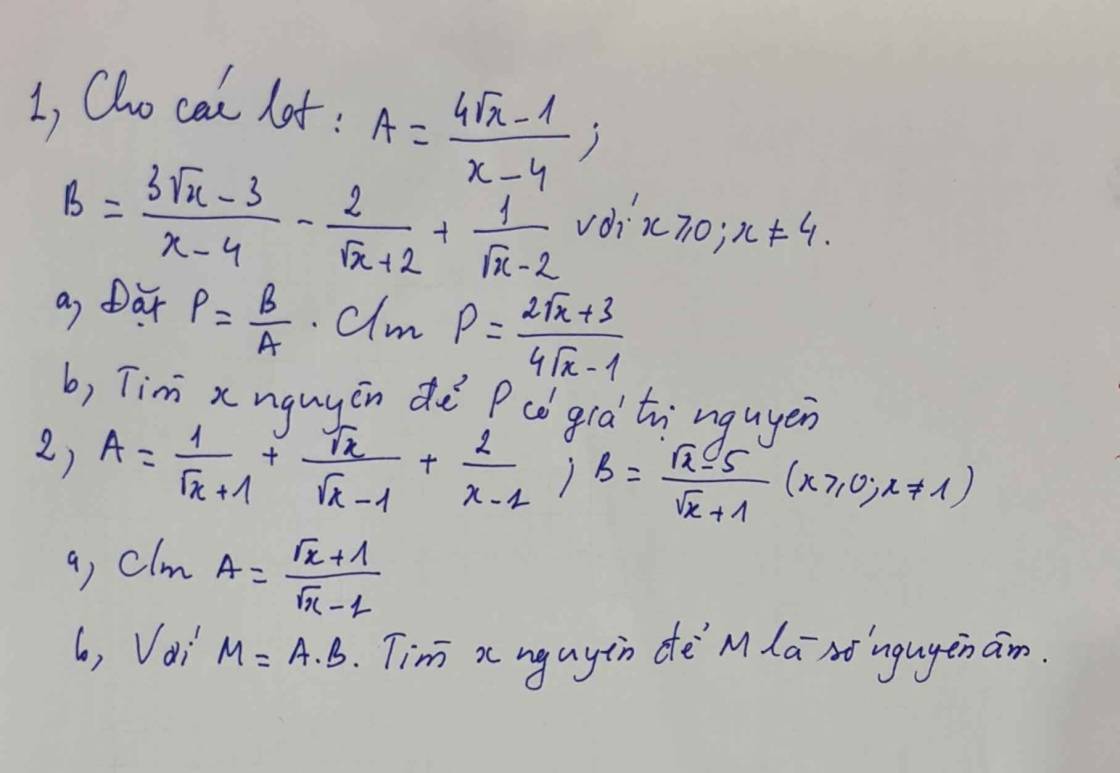
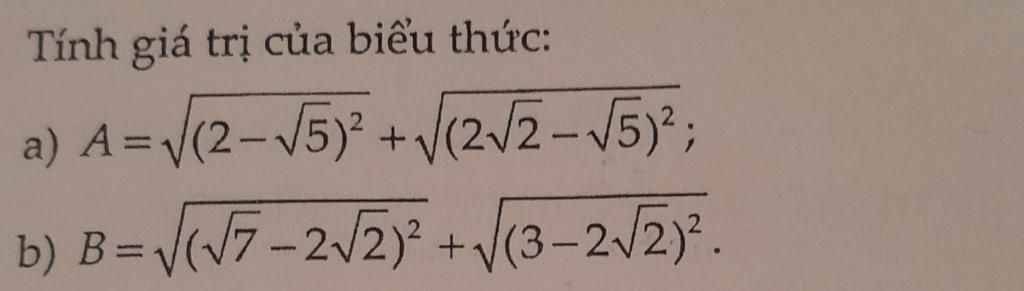
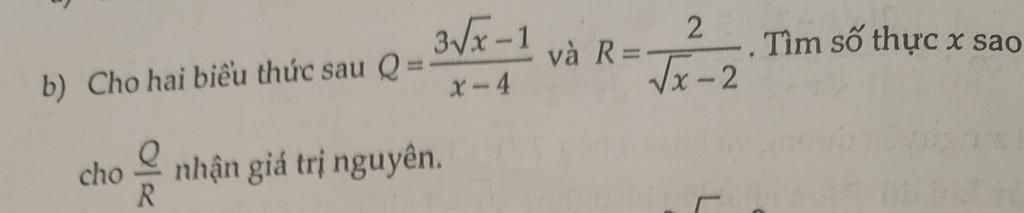
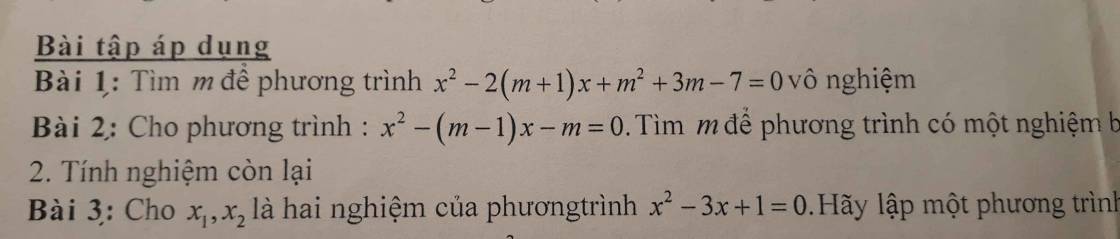
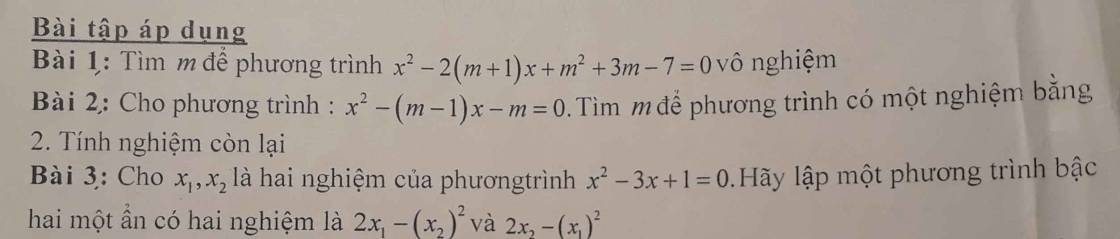
a: Vì (d)//y=3x nên m-1=3
hay m=2
Vậy: (d): y=3x+2n-5
Thay x=1 và y=4 vào (d), ta được:
2n-5+3=4
\(\Leftrightarrow2n=6\)
hay n=3