KL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CL
12 tháng 2 2020
Gọi tử số của phân số đó là:a.
Mẫu số của phân số đó là:b.
Ta có: a/b = 32/60 => a = 32/60xb
Mà: a+b=161
Thay a = 32/60xb vào a+b=161 ta được:
32/60xb+b=161
Quy đồng mẫu số, ta có:
32xb+60xb=161x60
92xb=9660
b=9660:92=105
Tử số là: 161-105=56
Vậy phân số đó là: 56/105.
SG
4
.9h sáng mai là em phải nộp bài rồi mà chưa biết giải
Em xin thề,ai giải giùm em(lời giải chi tiết
) em bái là sư phụ luôn
.Nhờ các bậc tiền bối chỉ bảo :
AT
5 tháng 7 2017
\(2\left(x-3\right)-3\left(1-2x\right)=4+4\left(1-x\right)\)
\(\Rightarrow2x-6-3+6x=4+4-4x\)
\(\Rightarrow2x+6x+4x=4+4+3+6\)
\(\Rightarrow12x=17\Rightarrow x=\dfrac{17}{12}\)
Vậy..................
5 tháng 7 2017
\(2\left(x-3\right)-3\left(1-2x\right)=4+4\left(1-x\right)\)
\(2x-6-3+6x=4+4-4x\)
\(8x-9=8-4x\)
\(8x=8-4x+9\)
\(8x=17-4x\)
\(12x=17\)
\(x=\dfrac{17}{12}\)
1 tháng 4 2017
Gọi số cần tìm là \(n\) \(\left(n\in N\right)\)
Vì \(n⋮5\) và \(n⋮27\)
\(\Rightarrow n\) có chữ số tận cùng là \(0\) hoặc \(5\)
+) Xét \(n=\)*\(975\) chia hết cho \(9\) \(\Rightarrow\) *\(=6\). Thử lại \(6975\) \(⋮̸\) \(27\) \(\rightarrow loại\)
+) Xét \(n=\)*\(970\) chia hết cho \(9\) \(\Rightarrow\) *\(=2\) Thử lại \(2970⋮27\) (TM)
Vậy \(n=2970\) là giá trị cần tìm
~~Chúc bn học tốt!!~~
1 tháng 4 2017
theo mk nghĩ là 27 = 3.9. C/m chia hết cho 27 thì c/m chia hết cho 3 và 9 nhưng mà ƯCLN(3,9)=3 kia mà. Bạn giải thích đoạn đó giúp mk đc ko?
T
9 tháng 4 2022
Câu 14)
\(a,\\ =-\dfrac{3}{8}+\dfrac{8}{17}+\dfrac{-5}{8}-\dfrac{3}{5}+\dfrac{9}{17}\\ =\left(\dfrac{-3}{8}+\dfrac{-5}{8}\right)+\left(\dfrac{8}{17}+\dfrac{9}{17}\right)-\dfrac{3}{5}\\ =\left(-1\right)+1-\dfrac{3}{5}=0-\dfrac{3}{5}=\dfrac{-3}{5}\\ b,\\ =\dfrac{7}{15}.\dfrac{-15}{14}+\left(\dfrac{27}{16}-\dfrac{1}{8}\right):\dfrac{5}{8}\)
\(=\dfrac{-1}{2}+\dfrac{25}{16}.\dfrac{8}{5}=\dfrac{-1}{2}+\dfrac{5}{2}=2\\ c,\\ =\dfrac{2}{2}-\dfrac{2}{3}+\dfrac{2}{3}-\dfrac{2}{4}+.....+\dfrac{2}{99}-\dfrac{2}{100}\\ =1-\dfrac{1}{50}=\dfrac{49}{50}\)
Câu 15
\(a,2x+\dfrac{-1}{4}=\dfrac{3}{2}\\ 2x=\dfrac{3}{2}-\dfrac{-1}{4}=\dfrac{7}{4}\\ x=\dfrac{7}{4}:2=\dfrac{7}{8}\\ b,\dfrac{15}{x}=\dfrac{-3}{4}\\ x=\dfrac{15.4}{-3}=-20\)
7 tháng 11 2017
\(\left(3n\right)^{100}\\ =3^{100}.n^{100}\\ =\left(3^4\right)^{25}.n^{100}\\ =81^{25}.n^{100}⋮81\)
Vậy \(\left(3n\right)^{100}⋮81\)
Chúc em học tốt!
17 tháng 4 2017
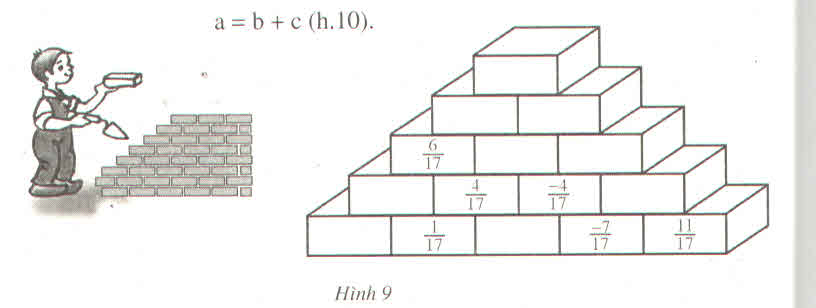
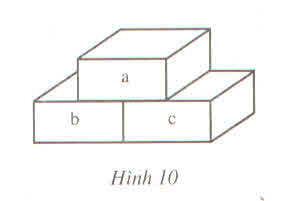
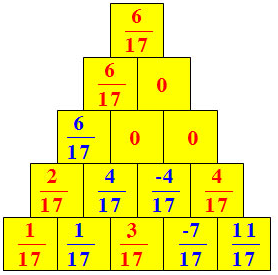
Làm theo quy tắc ở hình 10, ta có thể "xây tường" như sau:
SG
2
MH
23 tháng 6 2017
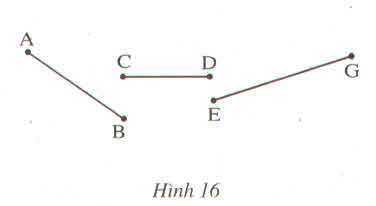
Muốn biết tổng độ dài các đoạn thẳng ở hình 16 trong 1 lần đo , ta dùng compa ''chuyển '' các đoạn thẳng AB ; CD; EG lên một đường thẳng sao cho mút C trùng mút B , mút E trùng mút D . Đo đoạn thẳng EG ta có :
AG = AB + CD + EG = 6 cm
Vậy tổng độ dài ba đoạn thẳng đó là 6 cm
Bài 5:
Ta có: \(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{49\cdot50}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
\(=\dfrac{49}{50}< 1\)