
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABE và ΔADC có
AB/AD=AE/AC
góc A chung
Do đó:ΔABE\(\sim\)ΔADC
b: Ta có: ΔABE\(\sim\)ΔADC
nên AB/AD=BE/DC
hay \(AB\cdot DC=AD\cdot BE\)

a) Xét 2 tam giác CKB và tam giác BAD có
Góc DAB = góc BKC = 90o
Góc ABD = góc CBD (BD là đường chéo hình chữ nhật ABCD => Tính chất)
=> Tam giác CKB đồng dạng với tam giác BAD

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: BC=căn 15^2+20^2=25cm
BH=AB^2/BC=15^2/25=9cm
c: Xét ΔBKH vuông tại K và ΔBAC vuông tại A có
góc B chung
=>ΔBKH đồng dạng với ΔBAC
=>S BKH/S BAC=(BH/BC)^2=(9/25)^2=81/625
=>S AKHC/S BAC=1-81/625=544/625
S ABC=1/2*AB*AC=1/2*15*20=150cm2
=>S AKHC=544/625*150=130,56cm2

a: Xét ΔAHD có
AP là đường cao ứng với cạnh HD
AP là đường trung tuyến ứng với cạnh HD
Do đó: ΔAHD cân tại A
mà AP là đường cao ứng với cạnh HD
nên AP là đường phân giác ứng với cạnh HD
Xét ΔAHE có
AQ là đường cao ứng với cạnh HE
AQ là đường trung tuyến ứng với cạnh HE
Do đó: ΔHAE cân tại A
mà AQ là đường cao ứng với cạnh HE
nên AQ là đường phân giác ứng với cạnh HE
Ta có: \(\widehat{EAD}=\widehat{EAH}+\widehat{DAH}\)
\(=2\left(\widehat{QAH}+\widehat{PAH}\right)\)
\(=2\cdot90^0=180^0\)
Do đó: E,A,D thẳng hàng
mà AD=AE(=AH)
nên A là trung điểm của DE
a) Xét \(\Delta ADP\) = \(\Delta AHP\) có: ( cạnh huyền -cạnh góc vuông)
góc APD = APH=90o
AD = AH
AP chung
=> AD=AH (1)
CMTT với \(\Delta AEQ=\Delta AHQ\left(CH-CGV\right)\)
=> AE= AH (2)
Từ 1 và 2 => AD= AE
=> A là trung điểm của DE
b) Xét \(\Delta DHE\) có:
DP=PH; HQ=QE
=> PQ là đg trung bình của tam giắc DHE
=> PQ// DE; PQ=1/2 DE
c) Xét tứ giác APHQ có: góc HPA= 90o; Góc A =90o; góc HQA=90o
=> Tứ giác APHQ là HCN
=> PQ=AH ( theo t/c HCN)

a: ΔABC vuông tại A
mà AM là trung tuyến
nên MA=MB=MC=BC/2
Xét ΔMAB có MA=MB và \(\widehat{MBA}=60^0\)
nên ΔMAB đều
b: ΔBAM đều
mà BH là đường cao
nên H là trung điểm của AM
Xét ΔHNM vuông tại H và ΔHBA vuông tại H có
HM=HA
\(\widehat{HMN}=\widehat{HAB}\)(MN//AB)
Do đó: ΔHNM=ΔHBA
=>HN=HB
=>H là trung điểm của BN
Xét tứ giác ABMN có
H là trung điểm chung của AM và BN
BM=BA
Do đó: ABMN là hình thoi
c: ABMN là hình thoi
=>\(\widehat{NMB}=180^0-\widehat{MBA}=180^0-60^0=120^0\)
Xét ΔMNB có \(cosNMB=\dfrac{MN^2+MB^2-BN^2}{2\cdot MN\cdot MB}\)
\(\Leftrightarrow\dfrac{AB^2+AB^2-BN^2}{2\cdot AB\cdot AB}=-\dfrac{1}{2}\)
=>\(2AB^2-BN^2=-AB^2\)
=>\(BN^2=3AB^2\)
Xét ΔMAC có \(cosAMC=\dfrac{MA^2+MC^2-AC^2}{2\cdot MA\cdot MC}\)
=>\(\dfrac{AB^2+AB^2-AC^2}{2\cdot AB\cdot AB}=cos120=\dfrac{-1}{2}\)
=>\(2AB^2-AC^2=-AB^2\)
=>\(AC^2=3AB^2\)
=>\(AC^2=BN^2\)
=>AC=BN
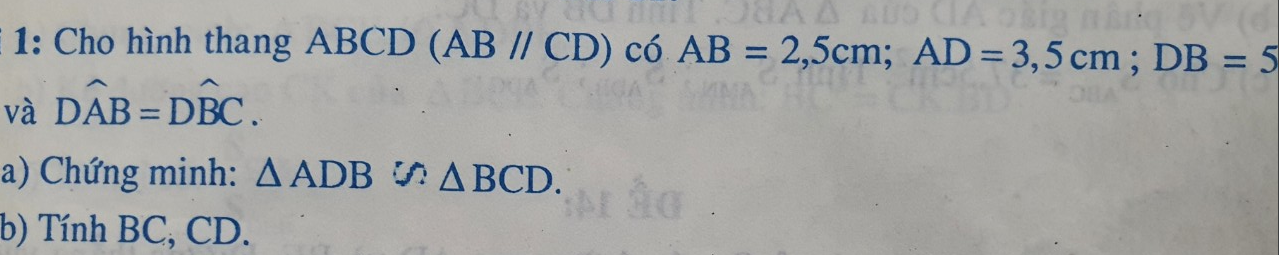








a: Xét ΔADB và ΔBCD có
góc DAB=góc CBD
góc ABD=góc BDC
=>ΔADB đồng dạng với ΔBCD
b: ΔADB đồng dạng với ΔBCD
=>AD/BC=DB/CD=AB/BD
=>3,5/BC=5/DC=2,5/5=1/2
=>BC=7cm; DC=10cm