K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1
1
9 tháng 10 2021
\(\left(\sqrt{5-2\sqrt{6}}+\sqrt{2}\right)\cdot\dfrac{1}{\sqrt{3}}\)
\(=\sqrt{3}\cdot\dfrac{1}{\sqrt{3}}\)
=1
9 tháng 10 2021
=\(\sqrt{2\left(12-6\sqrt{3}\right)}-\sqrt{2\left(28+10\sqrt{3}\right)}\)
=\(\sqrt{2\left(3-\sqrt{3}\right)2}-\sqrt{2\left(5+\sqrt{3}\right)^2}\)
=\(\sqrt{2}\left(3-\sqrt{3}\right)-\sqrt{2}\left(5+\sqrt{3}\right)=\sqrt{2}\left(3-\sqrt{3}-5-\sqrt{3}\right)\)
=\(\sqrt{2}\left(-2-2\sqrt{3}\right)\)=\(-2\sqrt{2}-2\sqrt{6}\)
22 tháng 4 2023
cái này áp dụng hệ thức lượng thôi bạn
AH=căn 6^2-4,8^2=3,6cm
=>AC=6^2/3,6=10cm
A
10 tháng 10
Độ dài ACACAC được tính từ góc A=6∘A = 6^\circA=6∘ và cạnh đối AH=305 mAH = 305 \, mAH=305m.
AC=AHsinA=305sin6∘AC = \frac{AH}{\sin A} = \frac{305}{\sin 6^\circ}AC=sinAAH=sin6∘305Độ dài CBCBCB được tính từ góc B=4∘B = 4^\circB=4∘ và cạnh đối HB=458 mHB = 458 \, mHB=458m.
CB=HBsinB=458sin4∘CB = \frac{HB}{\sin B} = \frac{458}{\sin 4^\circ}CB=sinBHB=sin4∘458Thời gian leo dốc từ AAA đến CCC:
tAC=AC4 km/ht_{AC} = \frac{AC}{4 \, km/h}tAC=4km/hACThời gian xuống dốc từ CCC đến BBB:
tCB=CB19 km/ht_{CB} = \frac{CB}{19 \, km/h}tCB=19km/hCBTổng thời gian di chuyển: ttotal=tAC+tCBt_{\text{total}} = t_{AC} + t_{CB}ttotal=tAC+tCBThời gian bạn Học đến trường bằng cách cộng tổng thời gian này vào thời gian khởi hành 6 giờ 45 phút.
NC
2
9 tháng 11 2021
Bài 1:
\(a,A=6\sqrt{2}-6\sqrt{2}+2\sqrt{5}=2\sqrt{5}\\ b,B=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+\sqrt{2}\\ c,=2\sqrt{3}-6\sqrt{3}+15\sqrt{3}-4\sqrt{3}=7\sqrt{3}\\ d,=1+6\sqrt{3}-\sqrt{3}-1=5\sqrt{3}\\ e,=4\sqrt{2}+\sqrt{2}-6\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)
Bài 2:
\(a,ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{2x-3}=5\Leftrightarrow2x-3=25\Leftrightarrow x=14\\ b,PT\Leftrightarrow x^2=\sqrt{\dfrac{98}{2}}=\sqrt{49}=7\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+1\right)=0\\ \Leftrightarrow\sqrt{x-3}=0\left(\sqrt{x+3}+1>0\right)\\ \Leftrightarrow x=3\\ d,ĐK:x\ge1\\ PT\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\\ \Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x=2\left(tm\right)\\ e,PT\Leftrightarrow2x-1=16\Leftrightarrow x=\dfrac{17}{2}\\ f,PT\Leftrightarrow\left|2x-1\right|=\sqrt{3}-1\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{3}-1\\2x-1=1-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\x=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)
9 tháng 11 2021
Bài 3:
\(a,Q=\dfrac{1+5}{3-1}=3\\ b,P=\dfrac{x+\sqrt{x}-6+x-2\sqrt{x}-3-x+4\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-3}\\ c,M=\dfrac{\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{3-\sqrt{x}}{\sqrt{x}+5}=\dfrac{-\sqrt{x}}{\sqrt{x}+5}\)
Vì \(-\sqrt{x}\le0;\sqrt{x}+5>0\) nên \(M< 0\)
Do đó \(\left|M\right|>\dfrac{1}{2}\Leftrightarrow M< -\dfrac{1}{2}\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}-5}{2\left(\sqrt{x}+5\right)}< 0\Leftrightarrow\sqrt{x}-5< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow0\le x< 25\)
Bài 4:
\(a,A=\dfrac{16+2\cdot4+5}{4-3}=29\\ b,B=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,P=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}+1}\\ P=\dfrac{\left(\sqrt{x}+1\right)^2+4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\\ P\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}=2\sqrt{4}=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)
NH
11 tháng 7 2023
\(\sqrt{x^2-2x\sqrt{11}+11}=10\)
\(< =>\sqrt{\left(x-\sqrt{11}\right)^2}=10\\ < =>\left|x-\sqrt{11}\right|=10\\ < =>\left[{}\begin{matrix}x-\sqrt{11}=10\\x-\sqrt{11}=-10\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=10+\sqrt{11}\\x=-10+\sqrt{11}\end{matrix}\right.\)
\(1-\sqrt{1+5x}=x\left(đk:x\ge-\dfrac{1}{5}\right)\\ < =>\sqrt{1+5x}=1-x\\ < =>\left\{{}\begin{matrix}1-x\ge0\\1+5x=1-2x+x^2\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}x\le1\\x^2-7x=0\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}x\le1\\x\left(x-7\right)=0\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}x\le1\\\left[{}\begin{matrix}x=0\left(tm\right)\\x=7\left(ktm\right)\end{matrix}\right.\end{matrix}\right.\\ < =>x=0\)
BD
1
22 tháng 7 2021
Câu 2:
Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)
a=1; b=-2m-2; \(c=m^2+4\)
\(\text{Δ}=b^2-4ac\)
\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)
\(=4m^2+8m+4-4m^2-16\)
=8m-12
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow8m>12\)
hay \(m>\dfrac{3}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)
Vì x1 là nghiệm của phương trình nên ta có:
\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)
\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)
\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)
\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)
\(\Leftrightarrow m^2+8m-20=0\)
Đến đây bạn tự tìm m là xong rồi
27 tháng 5 2022
\(\left(x+2\right)\left(\dfrac{360}{x}-6\right)=360\)
\(ĐK:x\ne0\)
\(\Leftrightarrow\left(x+2\right)\left(\dfrac{360-6x}{x}\right)=360\)
\(\Leftrightarrow360-6x+\dfrac{720-12x}{x}=360\)
\(\Leftrightarrow360x-6x^2+720-12x=360x\)
\(\Leftrightarrow6x^2+12x-720=0\)
\(\Delta=12^2-4.6.\left(-720\right)\)
\(=17424>0\)
`->` pt có 2 nghiệm
\(\left\{{}\begin{matrix}x_1=\dfrac{-12-\sqrt{17424}}{12}=-12\\x_2=\dfrac{-12+\sqrt{17424}}{12}=10\end{matrix}\right.\) ( tm )
Vậy \(S=\left\{-12;10\right\}\)
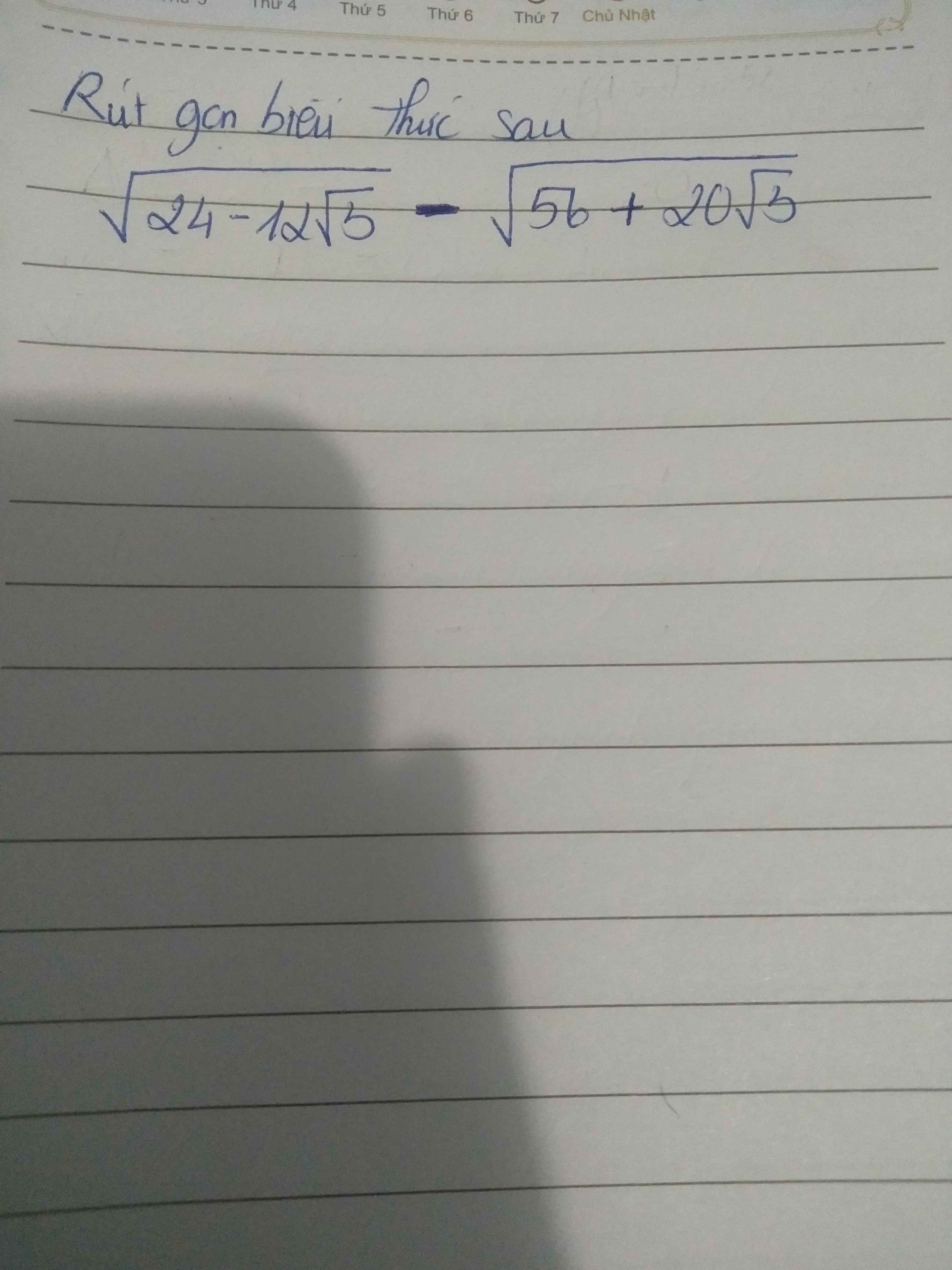
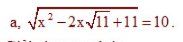
\(Q=x-2-2\sqrt{x-2}+4\)
\(=\left(\sqrt{x-2}-1\right)^2+3>=3\)
Dấu = xảy ra khi x=3
mik cảm mơn nhìu nha