K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 3 2022
a: Khi a=1 thì pt sẽ là \(\dfrac{x+1}{1-x}+\dfrac{x-1}{1+x}=\dfrac{1\cdot\left(3+1\right)}{1^2-x^2}\)
\(\Leftrightarrow\left(x+1\right)^2-\left(x-1\right)^2=4\)
=>4x=4
hay x=1(loại)
b: Vì x=1 thì \(a\in\varnothing\)
nên không có giá trị nào của a để pt nhận x=1 là nghiệm
7 tháng 11 2021
\(a,\Leftrightarrow x^2+2\cdot\dfrac{3}{2}x+\dfrac{9}{4}+\dfrac{3}{4}=0\\ \Leftrightarrow\left(x+\dfrac{3}{2}\right)^2+\dfrac{3}{4}=0\\ \Leftrightarrow\left(x+\dfrac{3}{2}\right)^2=-\dfrac{3}{4}\left(vô.lí\right)\\ \Leftrightarrow x\in\varnothing\\ b,\Leftrightarrow\left(2x-5\right)\left(2x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{5}{2}\end{matrix}\right.\)
15 tháng 1 2022
\(\Leftrightarrow a^2+b^2+c^2-ab-ac-bc>=0\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac>=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2>=0\)(luôn đúng)
15 tháng 1 2022
\(B=\dfrac{2x}{x-1}+\dfrac{5\left(x-1\right)\left(x+1\right)}{\left(x+1\right)^2}\cdot\dfrac{2\left(x+1\right)}{-5\left(x-1\right)}=\dfrac{2x}{x-1}-2=\dfrac{2x-2x+2}{x-1}=\dfrac{2}{x-1}\)
27 tháng 2 2022
Xét ΔPMN có PQ là đường phân giác
nên MQ/MP=NQ/NP
hay MQ/6,2=NQ/8,7
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{MQ}{6.2}=\dfrac{NQ}{8.7}=\dfrac{MQ+NQ}{6.2+8.7}=\dfrac{12.5}{14.9}=\dfrac{125}{149}\)
=>MQ=775/149(cm); NQ=2175/298(cm)
5 tháng 3 2022
a, Xét tam giác AMN và tam giác ABC có
^A _ chung
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{2,5}{7,5}=\dfrac{3}{9}=\dfrac{1}{3}\)
Vậy tam giác AMN ~ tam giác ABC (c.g.c)
b, Ta có tỉ số đồng dạng : \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\Rightarrow MN=\dfrac{AM.BC}{AB}=4cm\)
5 tháng 3 2022
a.Ta có:
\(\dfrac{AM}{AB}=\dfrac{2,5}{7,5}=\dfrac{1}{3};\dfrac{AN}{AC}=\dfrac{3}{9}=\dfrac{1}{3}\)
\(\Rightarrow\)MN//BC ( Ta-lét đảo )
=> Tam giác AMN đồng dạng tam giác ABC
b. Ta có: MN//BC ( cmt )
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MN}{BC}\)
\(\Leftrightarrow\dfrac{1}{3}=\dfrac{MN}{12}\)
\(\Leftrightarrow3MN=12\)
\(\Leftrightarrow MN=4cm\)
23 tháng 1 2022
a: AE=1/3AB=1/3x6=2(cm)
b: Xét ΔABC có EF//BC
nên AE/AB=AF/AC
c: Ta có: AE/AB=AF/AC
nên AF/8=1/3
=>AF=8/3(cm)
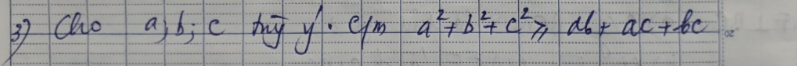
Gọi độ dài quãng đường AB là x
Theo đề, ta có phương trình: x/30-x/40=1/2
hay x=60