AN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AN
2
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 8 2021
Đặt \(x=\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\)
\(x^3=14-3\sqrt[3]{\left(\sqrt[]{50}+7\right)\left(\sqrt[]{50}-7\right)}\left(\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\right)\)
\(x^3=14-3x\)
\(x^3+3x-14=0\)
\(\left(x-2\right)\left(x^2+2x+7\right)=0\)
\(x=2\)
\(\Rightarrow\dfrac{m}{n}=2\)
\(\Rightarrow\) Hiển nhiên tồn tại vô số m, n nguyên thỏa mãn đẳng thức trên
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2022
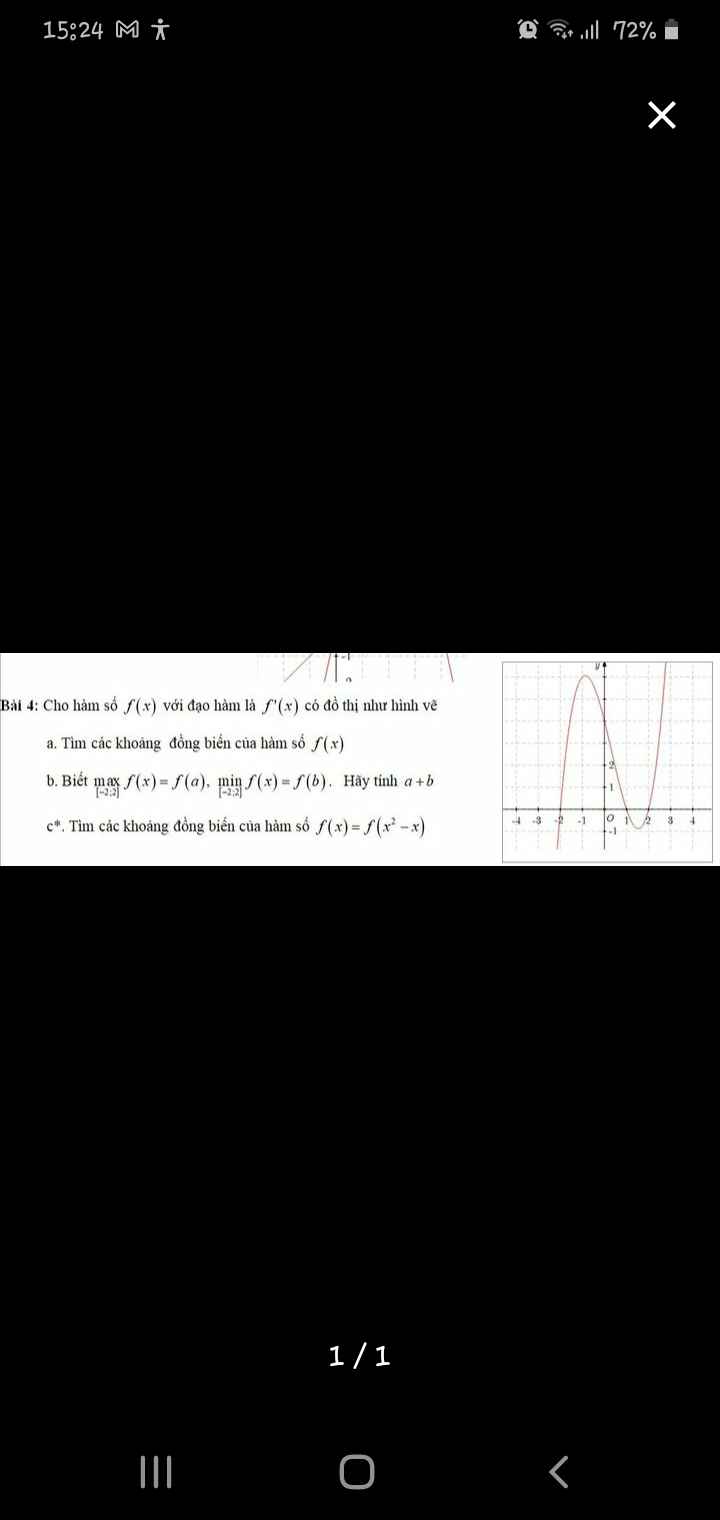
Từ đồ thị \(f'\left(x\right)\) ta có BBT hàm \(f\left(x\right)\) như sau:
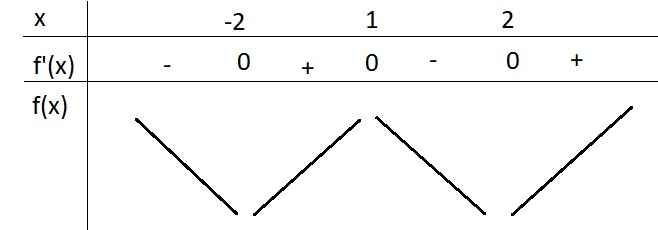
Từ đó ta thấy hàm \(f\left(x\right)\) đồng biến trên các khoảng \(\left(-2;1\right)\) và \(\left(2;+\infty\right)\)
Cũng từ BBT, trên \(\left[-2;2\right]\) ta thấy \(\max\limits_{\left[-2;2\right]}f\left(x\right)=f\left(1\right)\)
Diện tích giới hạn bởi phần đồ thị \(f'\left(x\right)\) và trục hoành trên \(\left[-2;1\right]\) lớn hơn đoạn \(\left[1;2\right]\)
\(\Rightarrow\int\limits^1_{-2}\left|f'\left(x\right)\right|dx>\int\limits^2_1\left|f'\left(x\right)\right|dx\Rightarrow\int\limits^1_{-2}f'\left(x\right)dx>\int\limits^1_2f'\left(x\right)dx\)
\(\Rightarrow f\left(1\right)-f\left(-2\right)>f\left(1\right)-f\left(2\right)\)
\(\Rightarrow f\left(2\right)>f\left(-2\right)\)
\(\Rightarrow\min\limits_{\left[-2;2\right]}f\left(x\right)=f\left(-2\right)\)
\(\Rightarrow a+b=1+\left(-2\right)=-1\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
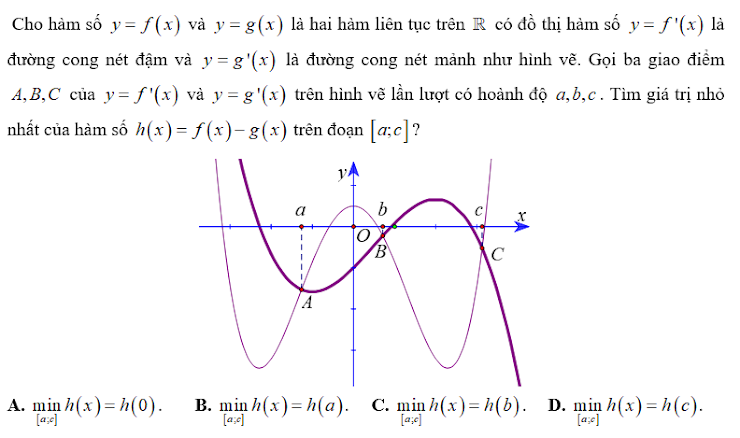
\(h'\left(x\right)=f'\left(x\right)-g'\left(x\right)=0\Rightarrow x=\left\{a;b;c\right\}\)
Ta thấy \(h'\left(x\right)>0\) trên \(\left(b;c\right)\) và \(h'\left(x\right)< 0\) trên \(\left(a;b\right)\)
\(\Rightarrow x=b\) là điểm cực tiểu trên \(\left[a;c\right]\) hay \(\min\limits_{\left[a;c\right]}h\left(x\right)=h\left(b\right)\)
TP
2
HT
28 tháng 2 2022
1b/ \(\overrightarrow{AB}=\left(1;1;3\right);\overrightarrow{u_{Oy}}=\left(0;1;0\right)\)
Vì \(\left(P_2\right)//AB//Oy\Rightarrow\overrightarrow{n_{\left(P_2\right)}}=\left[\overrightarrow{AB},\overrightarrow{u_{Oy}}\right]=\left(\left|\begin{matrix}1&3\\1&0\end{matrix}\right|,\left|\begin{matrix}3&1\\0&0\end{matrix}\right|,\left|\begin{matrix}1&1\\0&1\end{matrix}\right|\right)=\left(-3;0;1\right)\)
\(\Rightarrow\left(P_2\right):-3\left(x+3\right)+z-5=0\Leftrightarrow\left(P_2\right):3x-z+14=0\)
2b/
\(\overrightarrow{u_{Ox}}=\left(1;0;0\right);\overrightarrow{n_{\left(Q\right)}}=\left(3;2;5\right)\)
\(\Rightarrow\overrightarrow{n_{\left(\beta\right)}}=\left[\overrightarrow{u_{Ox}},\overrightarrow{n_{\left(Q\right)}}\right]=\left(0;-5;2\right)\)
\(d\left(O,\left(\beta\right)\right)=\dfrac{\left|d\right|}{\sqrt{25+4}}=\sqrt{29}\Rightarrow d=\pm29\)
\(\Rightarrow\left[{}\begin{matrix}\left(\beta\right):-5y+2z+29=0\\\left(\beta\right):-5y+2z-29=0\end{matrix}\right.\)
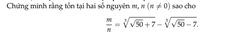
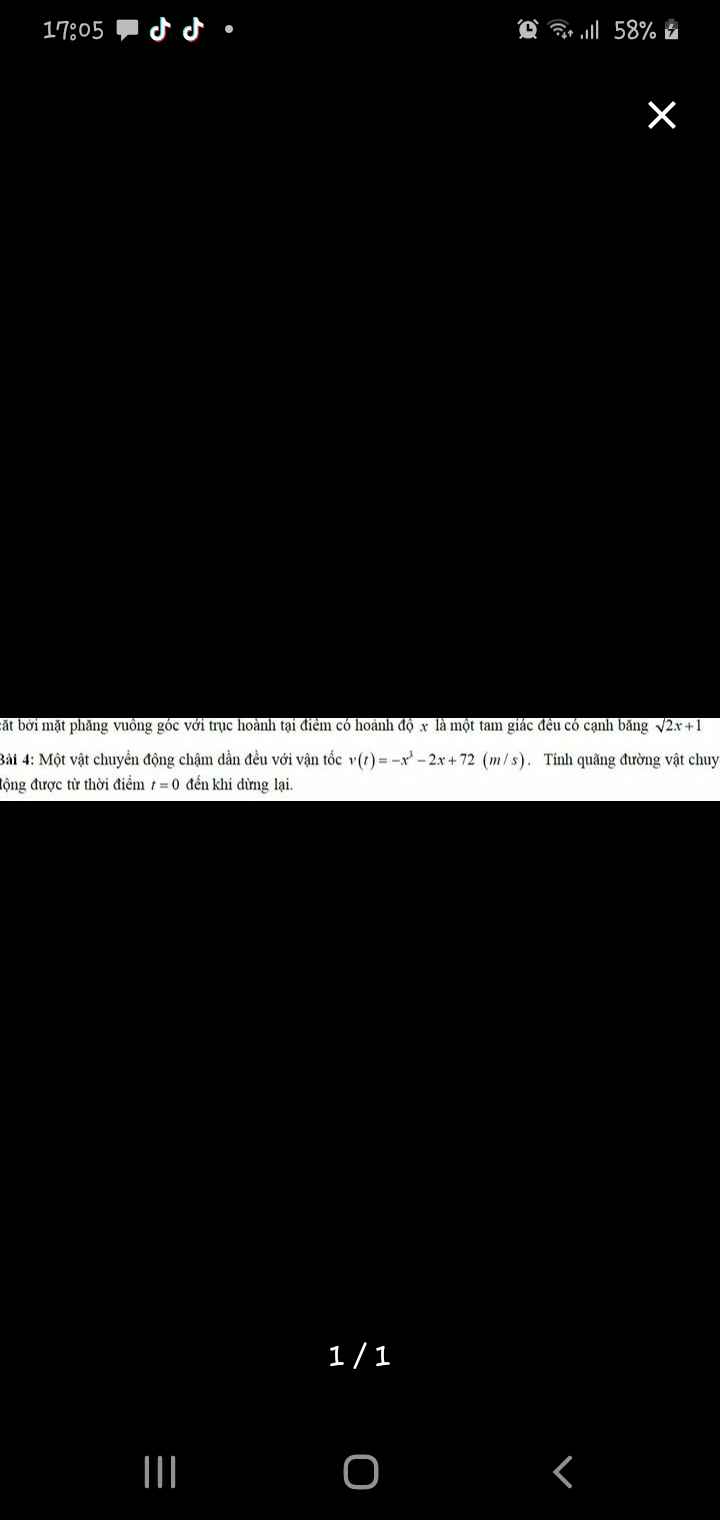Em muốn hỏi là có thể gọi mấy cái x ở trong v (t) là ẩn t không ạ vì dạng này em thấy về ẩn t nên gặp cái ẩn x nó hơi hoang mang ạ nếu đc mn gthich cho em với ạ em cảm ơn 😢
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2022
Việc gọi ẩn ko ảnh hưởng gì tới kết quả bài toán cả, cứ thoải mái đi
KM
0
Từ đồ thị ta thấy \(f'\left(x\right)>0\) trên các khoảng \(\left(-1;1\right)\) và \(\left(3;+\infty\right)\)
\(f'\left(x\right)< 0\) trên \(\left(-\infty;-1\right)\) và \(\left(1;3\right)\)
\(\Rightarrow\) Hàm nghịch biến trên (1;3)
Chọn B