ML
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 6 2021
(Dòng khoanh đỏ ở dấu tương đương đầu tiên)Có nghĩa là chia cả hai vế cho \(\dfrac{5\pi}{3}\) ấy
(Dòng khoanh đỏ ở dấu tương đương thứ hai) Xét \(cos\pi x=\dfrac{1}{10}+k\dfrac{6}{5}\) (*)
Do \(-1\le cos\pi x\le1\)\(\Leftrightarrow-1\le\dfrac{1}{10}+k\dfrac{6}{5}\le1\)
\(\Leftrightarrow-\dfrac{11}{12}\le k\le\dfrac{3}{4}\) mà k nguyên \(\Rightarrow k=0\)
Thay k=0 vào (*)\(\Rightarrow cos\pi x=\dfrac{1}{10}\)
Làm tương tự với cái bên dưới \(-1\le\dfrac{1}{2}+k\dfrac{6}{5}\le1\) \(\Leftrightarrow-\dfrac{5}{4}\le k\le\dfrac{5}{12}\Rightarrow\left[{}\begin{matrix}k=0\\k=-1\end{matrix}\right.\)
Thay k=0 với k=-1 sẽ ra được \(\left[{}\begin{matrix}cos\pi x=\dfrac{1}{2}\\cos\pi x=-\dfrac{7}{10}\end{matrix}\right.\)
(Với mỗi \(cos\pi x\) sẽ nhận được hai họ nghiệm => Tổng tất cả là 6 họ nghiệm)
HP
9 tháng 6 2021
Vì \(cosx\in\left[-1;1\right]\Rightarrow\left[{}\begin{matrix}-1\le\dfrac{1}{10}+k\dfrac{6}{5}\le1\left(1\right)\\-1\le\dfrac{1}{2}+k\dfrac{6}{5}\le1\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow-\dfrac{11}{12}\le k\le\dfrac{9}{12}\Leftrightarrow k=0\Rightarrow cosx=\dfrac{1}{10}\)
\(\left(2\right)\Leftrightarrow-\dfrac{15}{12}\le k\le\dfrac{5}{12}\Leftrightarrow\left[{}\begin{matrix}k=0\\k=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\\cosx=-\dfrac{7}{10}\end{matrix}\right.\)
27 tháng 7 2023
-1<=sin x<=1
=>-1<=-sin x<=1
=>2<=-sin x+3<=4
=>4<=(3-sin x)^2<=16
=>5<=y<=17
y min=5 khi 3-sin x=2
=>sin x=1
=>x=pi/2+k2pi
y max=17 khi 3-sin x=4
=>sin x=-1
=>x=-pi/2+k2pi
ML
1
1 tháng 9 2016
Chỗ khoanh bút bi thì là biến đổi tương đương từ biểu thức trước nó thôi bạn.
Còn chỗ khoanh mờ, là công thức nghiệm của hàm \(\cos x =0\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 8 2021
Đây là 1 lời giải sai em
Đơn giản vì phương trình gốc không thể giải được
E
0
7 tháng 6 2021
\(\dfrac{1}{2}sin6x\ne0\)\(\Leftrightarrow sin6x\ne0\) \(\Leftrightarrow6x\ne k\pi\)\(\Leftrightarrow x\ne\dfrac{k\pi}{6}\)
\(\dfrac{1}{2}\ne0\) rồi nên chỉ cần \(sin6x\ne0\)
DT
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2022
EG là đường trung bình tam giác MNP \(\Rightarrow\left\{{}\begin{matrix}EG||MN\\EG=\dfrac{1}{2}MN=x\end{matrix}\right.\)
FG là đường trung bình tam giác MPQ \(\Rightarrow\left\{{}\begin{matrix}FG=\dfrac{1}{2}PQ=x\sqrt{2}\\FG||PQ\end{matrix}\right.\)
\(\Rightarrow\widehat{\left(MN;PQ\right)}=\widehat{\left(EG;FG\right)}\)
\(cos\widehat{EGF}=\dfrac{EG^2+FG^2-EF^2}{2EG.FG}=-\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{EGF}=135^0\)
\(\Rightarrow\widehat{\left(MN;PQ\right)}=180^0-135^0=45^0\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9 2021
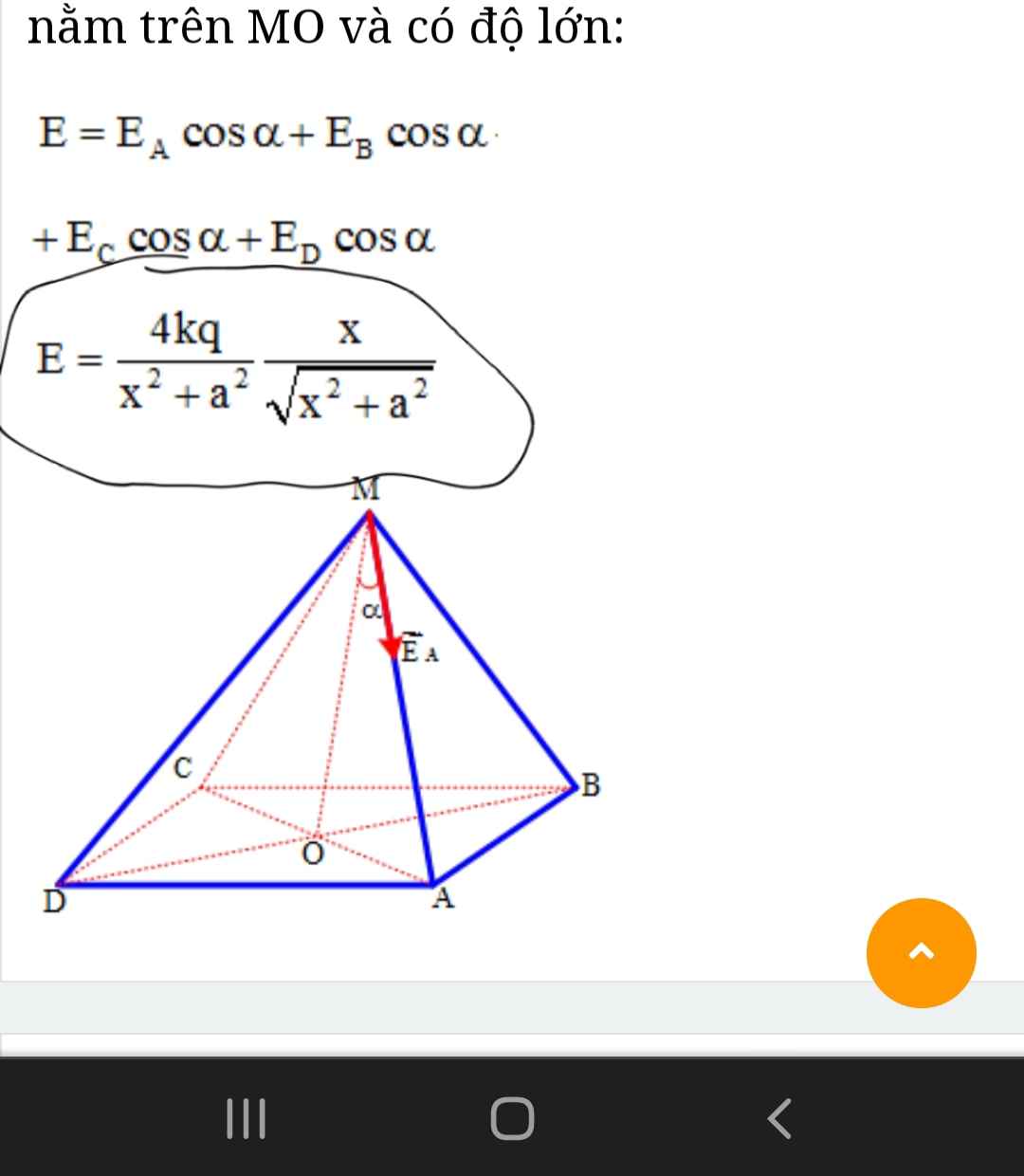
\(\dfrac{4kq.x}{\sqrt{\left(x^2+a^2\right)^3}}=\dfrac{4kq.x}{\sqrt{\left(x^2+\dfrac{a^2}{2}+\dfrac{a^2}{2}\right)^3}}\le\dfrac{4kq.x}{\sqrt{\dfrac{27.x^2.a^4}{4}}}=\dfrac{4kq.x}{\dfrac{3\sqrt{3}}{2}.x.a^2}=\dfrac{8\sqrt{3}.kq}{9a^2}\)
Dấu "=" xảy ra khi \(x=\dfrac{a}{\sqrt{2}}\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 6 2021
\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{3}=\dfrac{\pi}{6}+k2\pi\\2x+\dfrac{\pi}{3}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+k\pi\\x=\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất là \(x=\dfrac{\pi}{4}\approx0.79\)
Đáp án C