K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TA
6 tháng 8 2021
b) `sin^2 3x=1`
`<=> (1-cos6x)/2=1`
`<=> 1-cos6x=2`
`<=> cos6x=-1`
`<=> 6x=π +k2π`
`<=>x=π/6 +k π/3 ( k \in ZZ)`
c) `tan^2 2x=3`
`<=> (1-cos4x)/(1+cos4x)=3`
`<=> 1-cos4x=3+3cos4x`
`<=>cos4x = -1/2`
`<=>4x= \pm (2π)/3 +k2π`
`<=>x = \pm π/6 + k π/2 (k \in ZZ)`
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
3.
\(u_2=\dfrac{1}{2-u_1}=\dfrac{1}{2-\dfrac{1}{2}}=\dfrac{2}{3}\)
\(u_3=\dfrac{1}{2-u_2}=\dfrac{1}{2-\dfrac{2}{3}}=\dfrac{3}{4}\)
\(u_4=\dfrac{1}{2-\dfrac{3}{4}}=\dfrac{4}{5}\)
4.
\(u_1=\dfrac{2^{1+1}+1}{2^1}=\dfrac{5}{2}\)
\(u_3=\dfrac{2^4+1}{2^3}=\dfrac{17}{8}\)
\(u_5=\dfrac{2^6+1}{2^5}=\dfrac{65}{32}\)
5. Đề bị khuất
HP
10 tháng 9 2021
1.
a, \(sin2x-\sqrt{3}cos2x=-1\)
\(\Leftrightarrow\dfrac{1}{2}sin2x-\dfrac{\sqrt{3}}{2}cos2x=-\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{3}\right)=sin\left(-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{3}=-\dfrac{\pi}{6}+k2\pi\\2x-\dfrac{\pi}{3}=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}+k\pi\\x=\dfrac{3\pi}{4}+k\pi\end{matrix}\right.\)
10 tháng 9 2021
Do tổng các hệ số thứ 1,2,3 là 46 nên ta có:\(C_n^0+C_n^1+C_n^2=46\)
\(\Leftrightarrow1+\dfrac{n!}{1!\left(n-1\right)!}+\dfrac{n!}{2!\left(n-2\right)!}=46\)
\(\Leftrightarrow1+n+\dfrac{\left(n-1\right)n}{2}=46\)
\(\Leftrightarrow n^2+n-90=0\)
\(\Leftrightarrow\left[{}\begin{matrix}n=9\\n=-10\left(loai\right)\end{matrix}\right.\)
Khai triển biểu thức: \(\left(x+\dfrac{1}{x}\right)^9\)
Hạng tử thứ k+1 trong biểu thức trên
\(\left(x+\dfrac{1}{x}\right)^9=C_9^{k+1}+\left(x^2\right)^{10-k}.\left(\dfrac{1}{x}\right)^{k+1}\)
đến đây mình chịu rùi hjhj b nào làm được giúp b kia với
TD
14
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 6 2021
Tất cả k dưới đây đều là \(k\in Z\)
6.
\(\Leftrightarrow\sqrt{3}cot\left(3x-\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow cot\left(3x-\dfrac{\pi}{3}\right)=\dfrac{1}{\sqrt{3}}\)
\(\Leftrightarrow cot\left(3x-\dfrac{\pi}{3}\right)=cot\left(\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow3x-\dfrac{\pi}{3}=\dfrac{\pi}{3}+k\pi\)
\(\Leftrightarrow3x=\dfrac{2\pi}{3}+k\pi\)
\(\Leftrightarrow x=\dfrac{2\pi}{9}+\dfrac{k\pi}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 6 2021
7.
\(\Leftrightarrow\sqrt{3}tan\left(3x-15^0\right)=-1\)
\(\Leftrightarrow tan\left(3x-15^0\right)=-\dfrac{1}{\sqrt{3}}\)
\(\Leftrightarrow tan\left(3x-15^0\right)=tan\left(-30^0\right)\)
\(\Leftrightarrow3x-15^0=-30^0+k180^0\)
\(\Leftrightarrow3x=-15^0+k180^0\)
\(\Leftrightarrow x=-3^0+k60^0\)
GM
0
ND
1
12 tháng 10 2021
Giải thích các bước giải:
sin 2x=cos xsin 2x=cos x
⇔sin 2x=sin (π2−x)⇔sin 2x=sin (π2-x)
⇔⇔ ⎡⎢⎣2x=π2−x+k2π (k∈Z)2x=π−π2+x+k2π (k∈Z)[2x=π2−x+k2π (k∈Z)2x=π−π2+x+k2π (k∈Z)
⇔⇔ ⎡⎢⎣3x=π2+k2π (k∈Z)x=π2+k2π (k∈Z)[3x=π2+k2π (k∈Z)x=π2+k2π (k∈Z)
⇔⇔ ⎡⎢ ⎢⎣x=π6+k2π3 (k∈Z)x=π2+k2π (k∈Z)[x=π6+k2π3 (k∈Z)x=π2+k2π (k∈Z)
Vậy S={π6+k2π3 (k∈Z),π2+k2π (k∈Z)
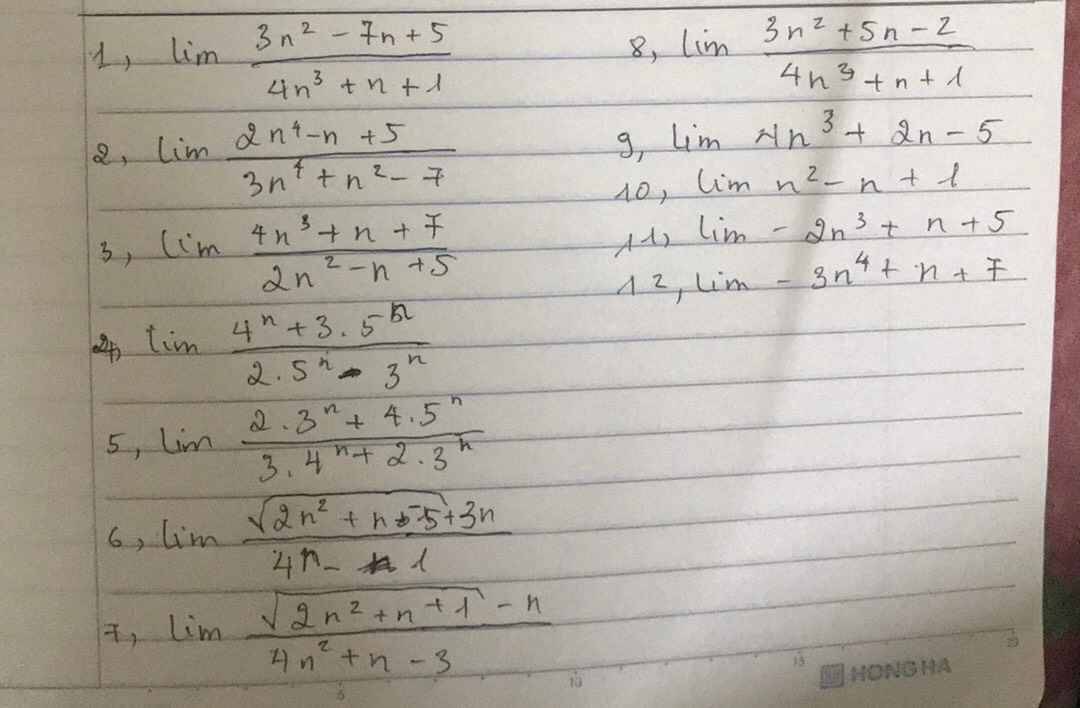
1: \(=lim\left(\dfrac{\dfrac{3}{n}-\dfrac{7}{n^2}+\dfrac{5}{n^3}}{4+\dfrac{1}{n^2}+\dfrac{1}{n^3}}\right)=0\)
2: \(=lim\left(\dfrac{2-\dfrac{1}{n^3}+\dfrac{5}{n^4}}{3+\dfrac{1}{n^2}-\dfrac{7}{n^4}}\right)=\dfrac{2}{3}\)
3: \(=lim\left(\dfrac{4+\dfrac{1}{n^2}+\dfrac{7}{n^3}}{\dfrac{2}{n}-\dfrac{1}{n^2}+\dfrac{5}{n^3}}\right)=+\infty\)
4: \(=lim\left(\dfrac{\left(\dfrac{4}{5}\right)^n+3}{2-\left(\dfrac{3}{5}\right)^n}\right)=\dfrac{3}{2}\)
5: \(=lim\left(\dfrac{2\cdot\left(\dfrac{3}{5}\right)^n+4}{3\cdot\left(\dfrac{4}{5}\right)^n+2\cdot\left(\dfrac{3}{5}\right)^n}\right)=+\infty\)
6: \(=lim\left(\dfrac{\sqrt{2+\dfrac{1}{n}-\dfrac{5}{n^2}}+3}{4-\dfrac{1}{n}}\right)=\dfrac{3}{4}\)
7: \(=lim\left(\dfrac{\sqrt{\dfrac{2}{n^2}+\dfrac{1}{n^3}+\dfrac{1}{n^4}}-\dfrac{1}{n}}{4+\dfrac{1}{n}-\dfrac{3}{n^2}}\right)=+\infty\)
\(8,lim\dfrac{3n^2+n-2}{4n^3+n+1}\)
\(=lim\dfrac{\dfrac{3n^2}{n^3}+\dfrac{n}{n^3}-\dfrac{2}{n^3}}{\dfrac{4n^3}{n^3}+\dfrac{n}{n^3}+\dfrac{1}{n^3}}\)
\(=lim\dfrac{\dfrac{3}{n}+\dfrac{1}{n^2}-\dfrac{2}{n^3}}{4+\dfrac{1}{n^2}+\dfrac{1}{n^3}}\)
\(=\dfrac{0}{4}\)
\(=0\)
\(9,lim4n^3+2n-5\)
\(=lim\left(\dfrac{4n^3}{n^3}+\dfrac{2n}{n^3}-\dfrac{5}{n^3}\right)\)
\(=lim\left(4+\dfrac{2}{n^2}-\dfrac{5}{n^3}\right)\)
\(=4\)
\(10,lim\left(n^2-n+1\right)\)
\(=lim\left(\dfrac{n^2}{n^2}-\dfrac{n}{n^2}+\dfrac{1}{n^2}\right)\)
\(=lim\left(1-\dfrac{1}{n}+\dfrac{1}{n^2}\right)\)
\(=1\)
\(11,lim\left(-2n^3+n+5\right)\)
\(=lim\left(-\dfrac{2n^3}{n^3}+\dfrac{n}{n^3}+\dfrac{5}{n^3}\right)\)
\(=lim\left(-2+\dfrac{1}{n^2}+\dfrac{5}{n^3}\right)\)
\(=-2\)
\(12,lim\left(-3n^4+n+7\right)\)
\(=lim\left(-\dfrac{3n^4}{n^4}+\dfrac{n}{n^4}+\dfrac{7}{n^4}\right)\)
\(=lim\left(-3+\dfrac{1}{n^3}+\dfrac{7}{n^4}\right)\)
\(=-3\)