K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MP
1
5 tháng 10 2021
Bài 2:
a: Ta có: \(M=2x\left(2x^3-3x\right)-x^2\left(3x^2-2\right)-x^2\left(x^2-4\right)\)
\(=4x^4-6x^2-3x^4+2x^2-x^4+4x^2\)
=0
b: Ta có: \(N=x\left(y^2-x\right)-y\left(xy-x^2\right)-x\left(xy-x-1\right)\)
\(=xy^2-x^2-xy^2+x^2y-x^2y+x^2+x\)
\(=x\)
OC
0
TN
0
15 tháng 1 2019
Lấy K là trung điểm CD thì HK là đường trung bình \(\Delta\)BCD => HK // BD và HK=BD/2
Từ HK=BD/2 và AH=BD/2 => \(\Delta\)AHK cân tại H => ^HAK = ^HKA. Mà ^HKA = ^ADB (Do HK //BD)
Nên ^HAK = ^ADB = ^ABC/2 + ^ACB hay ^BAC/2 = ^ABC/2 + ^ACB
<=> ^BAC = ^ABC + 2^ACB. Từ đó ta có hệ: \(\hept{\begin{cases}\widehat{BAC}=\widehat{ABC}+2\widehat{ACB}\\\widehat{ABC}+\widehat{BAC}+\widehat{ACB}=180^0\end{cases}}\)
Đến đây thì dễ rồi nhé !
31 tháng 7 2019
hiện nay An kém cha An 30 tuổi thì 3 năm trc An vẫn kém cha 30 tuổi
g/sử tuổi An 3 năm trc là a
=>a:2/7-a=30
=>a(7/2-1)=30
=>a.5/2=30
=>a=12
tuổi An hiện nay là 12+3=15
31 tháng 7 2019
Sau mấy năm thì An vẫn kém cha 30 tuổi vì hiệu ko bao giờ thay đổi
Tuổi An hiện nay là:
30 : (7 - 2) x 2 + 3 = 15 (tuổi )
Đáp số: 15 tuổi
KP
2 tháng 5 2022
cho mình hỏi đề bạn viết có đúng không vậy
Cho △ABC vuông tại A (AB<AC) có đường cao AH
a) Chứng minh : △HBA=△ABC ( chứng minh kiểu gì)
b)Chứng minh: AH2=HB.HC
c)Gọi E là điểm đối xứng với H qua điểm A, M là trung điểm của AH. Chứng minh CM⊥BE tại K
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 7 2021
\(B=\left(x-1\right)\left(x+6\right)\left(x+2\right)\left(x+3\right)\)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\)
\(B_{min}=-36\) khi \(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(C=\left(x^2-2x+1\right)+\left(y^2-4y+4\right)+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\)
\(C_{min}=2\) khi \(\left(x;y\right)=\left(1;2\right)\)
1 tháng 7 2021
b) Ta có: \(B=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\forall x\)
Dấu '=' xảy ra khi x(x+5)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy: \(B_{min}=-36\) khi \(x\in\left\{0;-5\right\}\)
c) Ta có: \(C=x^2-2x+y^2-4y+7\)
\(=x^2-2x+1+y^2-4y+4+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Vậy: \(C_{min}=2\) khi (x,y)=(1;2)
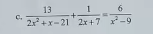
ĐKXĐ:\(\left\{{}\begin{matrix}x\ne-\dfrac{7}{2}\\x\ne3\end{matrix}\right.\)
\(\dfrac{13}{2x^2+x-21}+\dfrac{1}{2x+7}=\dfrac{6}{x^2-9}\\ \Leftrightarrow\dfrac{13}{2x^2-6x+7x-21}+\dfrac{1}{2x+7}=\dfrac{6}{\left(x-3\right)\left(x+3\right)}\)
\(\Leftrightarrow\dfrac{13}{2x\left(x-3\right)+7\left(x-3\right)}+\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(2x+7\right)\left(x+3\right)}-\dfrac{6\left(2x+7\right)}{\left(x-3\right)\left(x+3\right)\left(2x+7\right)}=0\)
\(\Leftrightarrow\dfrac{13\left(x+3\right)}{\left(2x+7\right)\left(x-3\right)\left(x+3\right)}+\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(2x+7\right)\left(x+3\right)}-\dfrac{6\left(2x+7\right)}{\left(x-3\right)\left(x+3\right)\left(2x+7\right)}=0\)
\(\Leftrightarrow\dfrac{13x+39+x^2-9-12x-42}{\left(2x+7\right)\left(x-3\right)\left(x+3\right)}=0\)
\(\Rightarrow x^2+x-12=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(ktm\right)\\x=-4\left(tm\right)\end{matrix}\right.\)