Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Nếu A, B, C thẳng hàng thì đường thẳng AB trùng đường thẳng AC, do đó hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương.
b) Nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì đường thẳng AB trùng đường thẳng AC, do đó ba điểm A, B, C có thẳng hàng.

a) Đúng.
Hai vec tơ đối nhau thì chúng có hoành độ đối nhau và tung độ đối nhau.
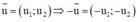
b) Sai.
Sửa lại: Vec tơ a→ cùng phương với vec tơ i→ nếu a→ có tung độ bằng 0.
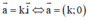
c) Đúng.
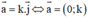

Lời giải:
Giả sử 3 vecto trên đôi một ngược hướng nhau
\(\overrightarrow{a}, \overrightarrow{b}\) ngược hướng
$\overrightarrow{c},\overrightarrow{b}$ ngược hướng
$\Rightarrow \overrightarrow{a}, \overrightarrow{c}$ cùng ngược hướng với $\overrightarrow{b}$
$\Rightarrow \overrightarrow{a}, \overrightarrow{c}$ cùng hướng (trái giả sử)
Vậy ít nhất 2 trong số 3 vecto cùng hướng.

Ta có: \(\overrightarrow{F}=\overrightarrow{F1}+\overrightarrow{F2}\) (1)
\(\Rightarrow\) \(F=\sqrt{F1^2+F2^2+2F1\cdot F2\cdot cos60^o}\) (Bình phương 2 vế của (1) r biến đổi vectơ F1, F2)
Chúc bn học tốt!

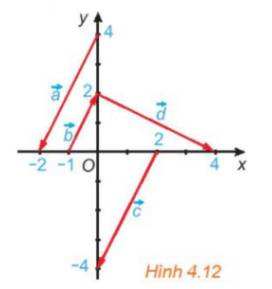
Dễ thấy giá của \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) song song với nhau.
Các vecto cùng phương là: \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)
Trong đó cặp vecto cùng hướng là \(\overrightarrow a ,\overrightarrow c \).
Cặp vecto ngược hướng là: \(\overrightarrow a ,\overrightarrow b \) và \(\overrightarrow b ,\overrightarrow c \).
Cặp vecto bằng nhau là: \(\overrightarrow a ,\overrightarrow c \)
Hai vecto cùng phương với 1 vecto thứ 3 khác \(\overrightarrow{0}\) thì cùng phương