Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số bạn trong lớp là \(n = 5 + 7 + 10 + 8 + 6 = 36\)
Thời gian chạy trung bình cự li 100 m của các bạn trong lớp là
\(\bar X = \frac{{5.12 + 7.13 + 10.14 + 8.15 + 6.16}}{{36}}\)
Chú ý
Bài toán này cho dưới dạng bảng tần số nên cần tính theo công thức trên.

a) Kết quả trung bình của 2 bạn là bằng nhau: \(\overline {{x_H}} = \overline {{x_T}} = 2,5\) (m)
b) +) Phương sai mẫu số liệu thống kê của bạn Hùng và Trung là:
\(s_H^2 = \frac{{{{\left( {2,4 - \overline {{x_H}} } \right)}^2} + {{\left( {2,6 - \overline {{x_H}} } \right)}^2} + {{\left( {2,4 - \overline {{x_H}} } \right)}^2} + {{\left( {2,5 - \overline {{x_H}} } \right)}^2} + {{\left( {2,6 - \overline {{x_H}} } \right)}^2}}}{5} = 0,008\)
\(s_T^2 = \frac{{{{\left( {2,4 - \overline {{x_H}} } \right)}^2} + {{\left( {2,5 - \overline {{x_H}} } \right)}^2} + {{\left( {2,5 - \overline {{x_H}} } \right)}^2} + {{\left( {2,5 - \overline {{x_H}} } \right)}^2} + {{\left( {2,6 - \overline {{x_H}} } \right)}^2}}}{5} = 0,004\)
+) 0,004 < 0,008 nên ta kết luận: Kết quả nhảy xa của bạn Trung ổn định.

Chọn A.
Giả sử các giá trị của mẫu số liệu là a; b; c; d với 0 < a < b < c < d và a; b; c;d là số tự nhiên.
+ Ta có 
Mà số trung bình là 6 nên a + b + c + d = 24
Suy ra a + d = 14
+ Ta có 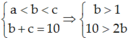 hay 1 < b < 5 mà b là số tự nhiên nên b = 2; 3; 4
hay 1 < b < 5 mà b là số tự nhiên nên b = 2; 3; 4
+ Nếu b = 2 thì c = 8, mà 0 < a < b; a là số tự nhiên nên a = 1 và d = 13
Khi đó các giá trị của mẫu số liệu là 1; 2; 8; 13
+ Nếu b = 3 thì c = 7, mà 0 < a < b; a số tự nhiên nên có 2 khả năng xảy ra: a = 1 ; d = 13 hoặc a = 2 ; d = 12
Khi đó có hai mẫu số liệu thỏa đề bài có giá trị là 1;3;7;13 và 2;3;7;12
+ Nếu b = 4 thì c = 6, mà 0 < a < b; a là số tự nhiên nên có 3 khả năng xảy ra:
a = 1; d = 13 hoặc a = 2 ; d = 12 hoặc a = 3 ; d = 11
Khi đó có ba mẫu số liệu thỏa đề bài có giá trị là 1;4;6;13 hoặc 2;4;6;12 hoặc 3;4;6;11
Suy ra với mẫu số liệu có các giá trị là 3;4;6;11 thì hiệu của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đạt giá trị nhỏ nhất.

Trong dãy số liệu thống kê trên có 20 giá trị ( không phân biệt) nên có tất cả 20 vận động viên tham gia chạy.
Vậy kích thước mẫu là 20
Chọn B.

Chọn B.
Điều tra thời gian hoàn thành một sản phẩm của 12 công nhân nên kích thước mẫu là 22.

Trong mẫu số liệu trên; các giá trị 15; 13; 16 đều xuất hiện nhiều nhất – là 3 lần.
Do đó; mốt của mẫu số liệu trên là : 15; 13; 16
Chọn D

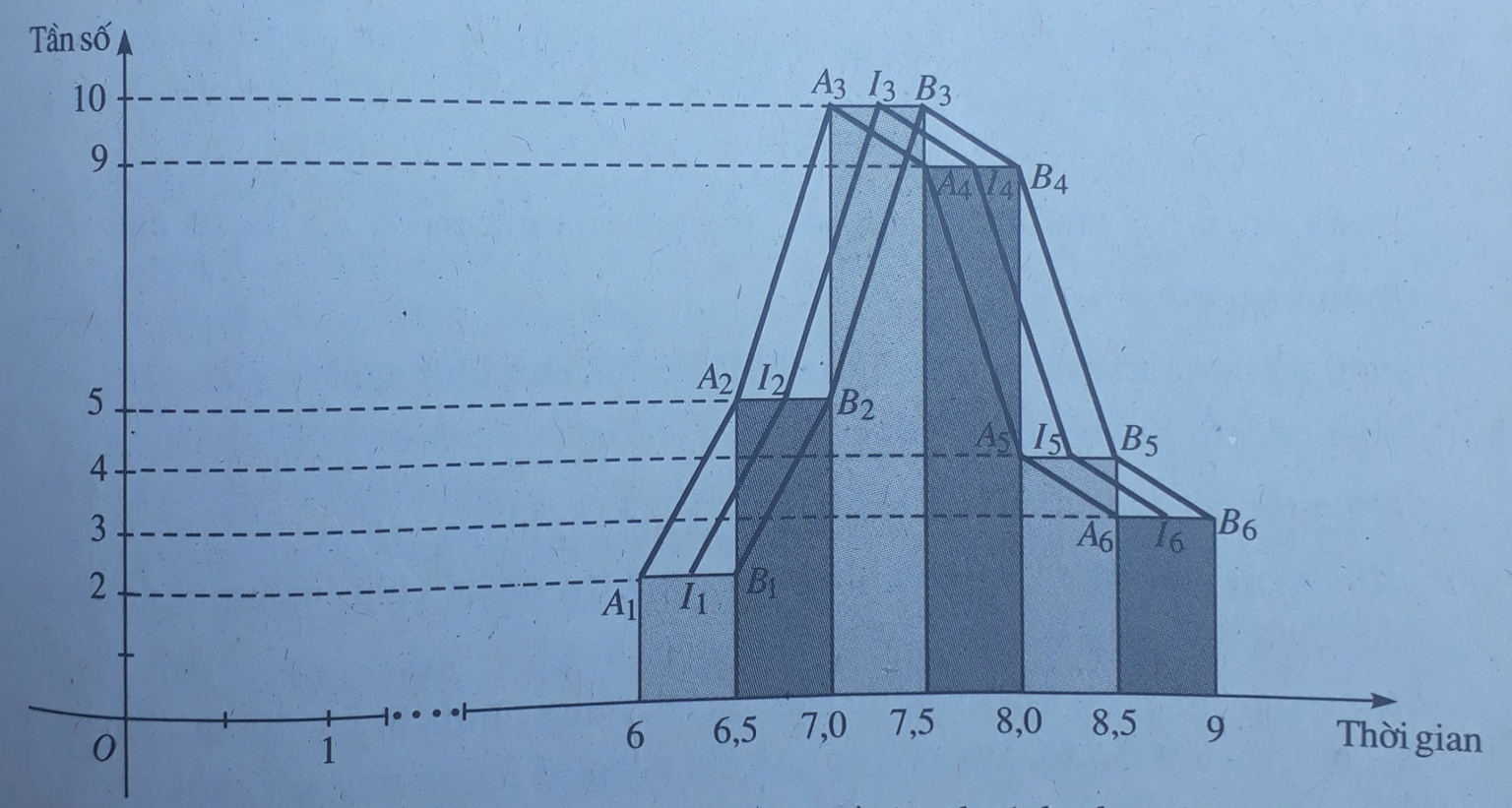
Các đỉnh của đường gấp khúc tần số có tọa độ là ( c i ; n i ), với c i là giá trị đại diện của lớp thứ i, n i là tần số của lớp thứ i. Từ đó suy ra: các đỉnh của đường gấp khúc tần số là các trung điểm của các cạnh phía trên của các cột (các hình chữ nhật) của biểu đồ tần số hình cột
Đường gấp khúc I 1 I 2 I 3 I 4 I 5 I 6 với I 1 , I 2 , I 3 , I 4 , I 5 , I 6 lần lượt là trung điểm của các đoạn thẳng A 1 B 1 , A 2 B 2 , A 3 B 3 , A 4 B 4 , A 5 B 5 , A 6 B 6

*) Sắp xếp thứ tự của mẫu số liệu theo thứ tự không giảm ta được: 1 2 4 5 9 10 11
a) Số trung bình cộng của mẫu số liệu trên là: \(\overline x = \frac{{1{\rm{ + }}2{\rm{ + }}4{\rm{ + }}5{\rm{ + }}9{\rm{ + }}10{\rm{ + }}11}}{7} = 6\)
b) Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 7 số liệu ( lẻ ) nên trung vị \({Q_2} = 5\)
c) Tứ phân vị của mẫu số liệu trên là:
Trung vị của dãy 1, 2, 4 là: \({Q_1} = 2\)
Trung vị của dãy 9, 10, 11 là: \({Q_3} = 10\)
Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 2\), \({Q_2} = 5\), \({Q_3} = 10\)
d) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 11 - 1 = 10\)
e) Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 10 - 2 = 8\)
g) Phương sai của mẫu số liệu trên là: \({s^2} = \frac{{\left[ {{{\left( {1 - \overline x } \right)}^2} + {{\left( {2 - \overline x } \right)}^2} + ... + {{\left( {11 - \overline x } \right)}^2}} \right]}}{7} = \frac{{96}}{7}\)
h) Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} = \sqrt {\frac{{96}}{7}} \)

Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
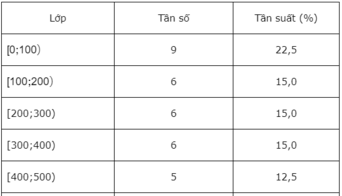
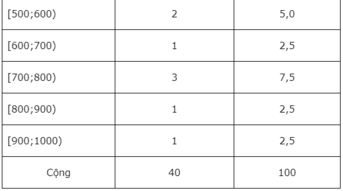
c) Cộng các tần suất của năm lớp [500;600), [600;700), [700;800), [800;900) và [900;1000) ta được . Đáp án là B.
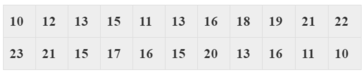


+) Ta có: \(\overline {{x_5}} = 57,96,\overline {{x_6}} = 272,04\)
+) Vậy phương sai của mẫu (5) và (6) là:
\(s_{\left( 5 \right)}^2 = \frac{{{{\left( {55,2 - \overline {{x_5}} } \right)}^2} + {{\left( {58,8 - \overline {{x_5}} } \right)}^2} + {{\left( {62,4 - \overline {{x_5}} } \right)}^2} + {{\left( {54 - \overline {{x_5}} } \right)}^2} + {{\left( {59,4 - \overline {{x_5}} } \right)}^2}}}{5} = 9,16\)
\(s_{\left( 6 \right)}^2 = \frac{{{{\left( {271,2 - \overline {{x_6}} } \right)}^2} + {{\left( {261 - \overline {{x_6}} } \right)}^2} + {{\left( {276 - \overline {{x_6}} } \right)}^2} + {{\left( {282 - \overline {{x_6}} } \right)}^2} + {{\left( {270 - \overline {{x_6}} } \right)}^2}}}{5} = 48,33\)
Nhận xét: Cự li chạy 500m có kết quả đồng đều hơn.