Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Phương pháp:
+ Xác định chiều cao của hình chóp
+ Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp:
Bước 1: Xác định tâm đường tròn ngoại tiếp hình vuông ABCD
Bước 2: Xác định trục đường tròn ngoại tiếp đa giác đáy. Kẻ đường trung trực một cạnh bên giao với trục đường tròn ở đâu đó chính là tâm mặt cầu ngoại tiếp hình chóp.
+ Tính bán kính mặt cầu ngoại tiếp hình chóp dựa vào định lý Pytago.
+ Mặt cầu có bán kính R thì có diện tích là S = 4 π R 2
Cách giải:
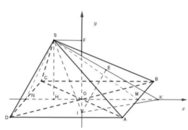
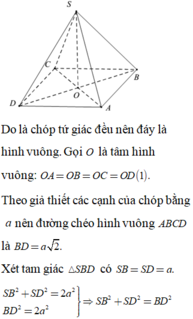
Gọi O là tâm hình vuông ABCD, gọi M , N lần lượt là trung điểm của AB; CD .
Kẻ SH ⊥ MN tại H .
Ta có SN ⊥ DC ; MN ⊥ DC
⇒ DC ⊥ ( SMN )
⇒ DC ⊥ SH
Mà SH ⊥ MN
⇒ SH ⊥ (ABCD).
Vì ABCD là hình vuông cạnh a nên:
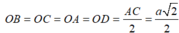
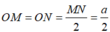
Vì tam giác SDC vuông cân tại S có cạnh huyền CD = a
⇒ SN= a 2
Vì tam giác ABS đều cạnh a
⇒ SM = a 3 2
Xét tam giác SNM có:
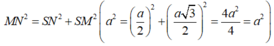
⇒ △ S M N vuông tại S.
Suy ra:
![]()
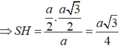
![]()
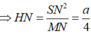
![]()
Nhận thấy O là tâm đường tròn ngoại tiếp hình vuông ABCD .
Kẻ tia Oy / /SH , khi đó tâm mặt cầu ngoại tiếp hình chóp S . ABCD nằm trên đường thẳng Oy.
Trên tia OM ta lấy K sao cho OK = OA = a 2 2 , khi đó K ∈ (O; OA)
Trong mặt phẳng (SMN ), lấy E là trung điểm SK , kẻ EI là đường trung trực của SK (I ∈ Oy).
Khi đó:
IK = IS = IA = IB = IC = ID nên I là tâm mặt cầu ngoại tiếp hình chóp S . ABCD và bán kính là R = IK.
Kẻ SF ⊥ Oy

Gắn hệ trục Oxy với OM ≡ Ox; Oy / /SH
Đặt I ( 0 , y o )
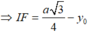
Xét tam giác vuông ISF có:
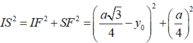
Xét tam giác vuông OIK có:
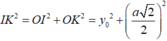
Vì ![]()

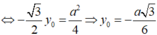
Suy ra bán kính mặt cầu:
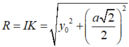
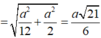
Diện tích mặt cầu ngoại tiếp hình chóp là:

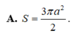
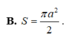
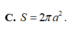

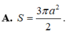

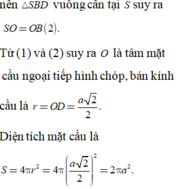


Đáp án C