Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) giá trị của un rất lớn khi n tăng lên vô hạn
b) Cần n > 384.1010 tờ giấy để đạt được những chồng giấy có về dày lớn hơn khoảng cách từ Trái Đất tới Mặt Trăng

Gọi `u` là số tiền phải trả khi thuê năm đầu tiên của công ty `A`.
Ta có CTTQ: `S_n =n u_1 +[n(n-1)]/2 .d`
`@` Công ty `B`.
Có: `10` năm `=40` quý
`15` năm `=60` quý
- Mảnh đất `1` thuê trong `10` năm là:
`S_[40]=40.8+[40.39]/2 .0,5=710` (triệu đồng)
- Mảnh đất `2` thuê trong `15` năm là:
`S_[60]=60.8+[60.59]/2 .0,5=1365` (triệu đồng)
`@` Công ty `C`.
- Mảnh đất `1` thuê trong `10` năm là:
`S_[10]=10.60+[10.9]/2 .3=735` (triệu đồng)
- Mảnh đất `2` thuê trong `15` năm là:
`S_[15]=15.60+[15.14]/2 .3=1215` (triệu đồng)
`->\bb D`.

(mấy bn vẽ hình minh họa cho dễ hỉu nha!)
vậy DT hình vuông tại điểm giao nhau giữa phân tăng thêm là 5x5= 25m2
DT phần còn lại khi đã trừ hình vuông là: 385-25= 360m2
vậy ta còn hai hình chữ nhật ( HCN dài, HCN ngắn)
theo đề bài, chiều dài gấp 3 chiều rộng nên:
chiều dài hình chữ nhật lúc đầu là là: 360 : (3+1) x 3 = 270m
chiều rộng là: 270 : 3 = 90m
DT HCN lúc đầu là: 270x90= 24300 m2
Gọi kích thước ban đầu của hcn theo chiều dài chiều rộng là x(m), y(m)
Theo đề ta có:
x=3y (1)
(x+5).(y+5)=xy+385 (2)
Thay (1) vào (2) => (3y+5)(y+5)=(3y)y+385
=> 3y²+15y+5y+25=3y²+385
=>20y=360
=> y=18
Thay y=18 vào (1) => x= 54
Vậy kích thước ban đầu hcn là 54m và 18m

Ta có: mặt phẳng chứa phần bàn và mặt phẳng chứa dao cắt, đường cắt chính là giao tuyến của hai mặt phẳng đó.
Giao tuyến của hai mặt phẳng là một đường thẳng nên đường cắt luôn là đường thẳng.

a. Mỗi cách xắp sêp 4 bạn vào 4 chỗ ngồi là một hoán vị của 4 phần tử. Vì vậy số phần tử của không gian mẫu là 4! =24
Chọn B

c. Trường hợp 1: bạn nam ngồi đầu. khi dó 2 bạn nam xếp vào 2 chỗ ( số ghế 1 và 3), nữ xếp nốt vào hai chỗ còn lại ( ghế số 2 và 4), số cách xếp là 2!.2!=4
Trường hợp 2: bnạ nữ ngồi đầu. Tương tự có 4 cách xếp . Vậy theo quy tắc cộng số phần tử của biến cố N là 4+4=8
Chọn C

b. đánh số ghế theo thứ tự 1,2,3,4. Hai bạn nam ngồi cạnh nhau ở vị trí ( 1 và 2) hoặc (2 và 3) hoặc (3 và 4). Nếu hai bạn nam đổi chỗ cho nhau( giữ nguyên chỗ hai bạn nữ) thì Ta có một cách xếp mới . vì vậy cần chọn phương án D
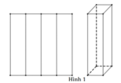
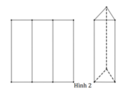
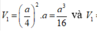
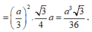
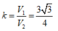

Mỗi lần cắt một mảnh giấy thành 7 mảnh, tức là Mạnh tạo thêm 6 mảnh giấy. Do đó công thức tính số mảnh giấy theo n bước được thực hiện là Sn = 6n + 1. Ta chứng minh tính đúng đắn của công thức trên bằng phương pháp quy nạp theo n.
Bước cơ sở. Mạnh cắt mảnh giấy thành 7 mảnh, n =1, S(1) = 6.1+1 =7
Công thức đúng với n = 1
Bước quy nạp: giả sử sau k bước, Mạnh nhận được số mảnh giấy là S(k) = 6k + 1
Sang bước thứ k +1, Mạnh lấy một trong số những mảnh giấy nhận được trong k bước trước và cắt thành 7 mảnh. Tức là Mạnh đã lấy đi 1 trong S(k) mảnh và thay vào đó 7 mảnh được cắt ra. Vậy tổng số mảnh giấy ở bước k + 1 là: S(k =1) = S(k) -1 + 7= S(k) + 6 = 6k + 1 + 1 = 6(k+1) +1
Vậy công thức S(n) đúng với mọi n ∈N* . Theo công thức trên chỉ có phương án D thoả mãn vì 121 =6.20 + 1
Đáp án D