K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 1 2017
\(\hept{\begin{cases}mx+my=-3\\\left(1-m\right)x+y=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}mx+m.\left(m-1\right)x=-3\\y=\left(m-1\right)x\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m^2x=-3\\y=\left(m-1\right)x\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{-3}{m^2}\\y=\left(m-1\right).\frac{-3}{m^2}\end{cases}}\)
Để phương trình có nghiệm âm thì ta có
\(\hept{\begin{cases}\frac{-3}{m^2}< 0\\\frac{-3.\left(m-1\right)}{m^2}< 0\end{cases}}\Leftrightarrow m>1\)
PM
1
26 tháng 10 2021
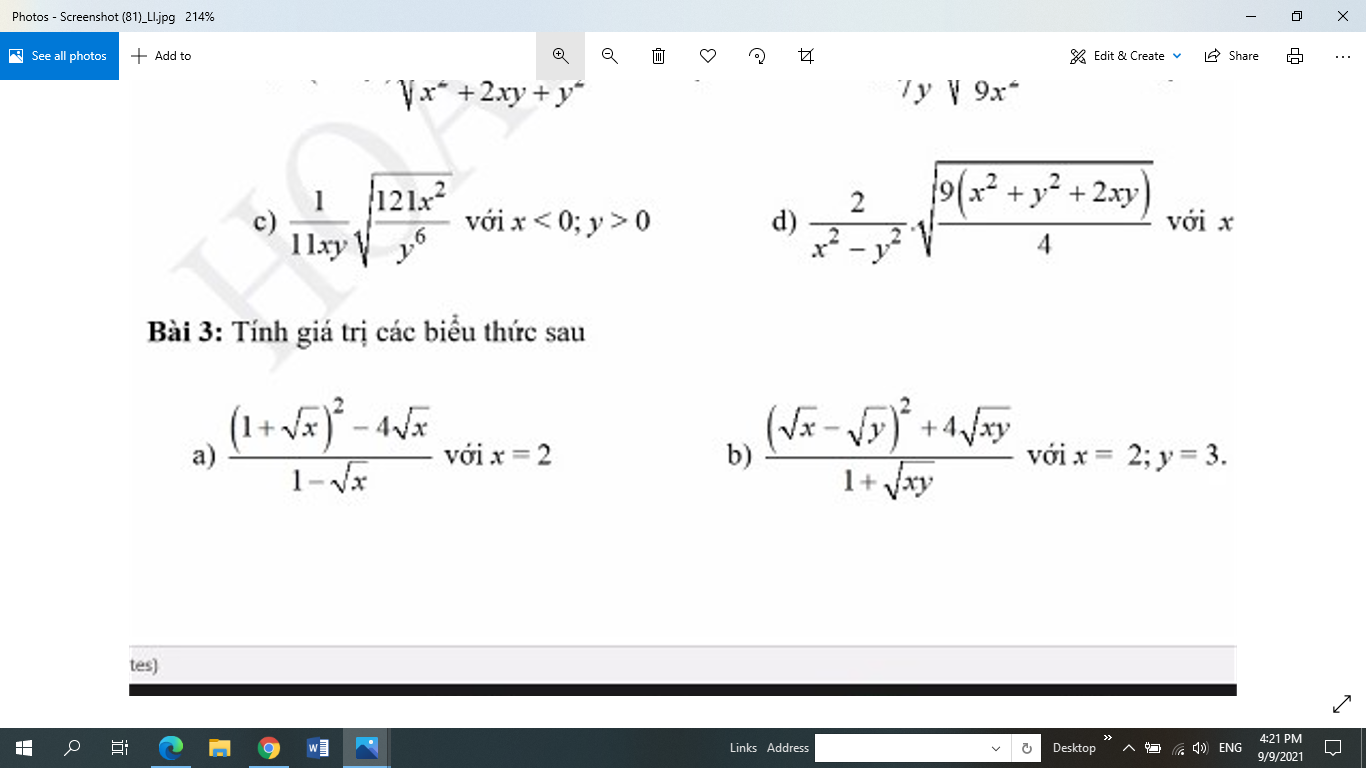
Bài 3:
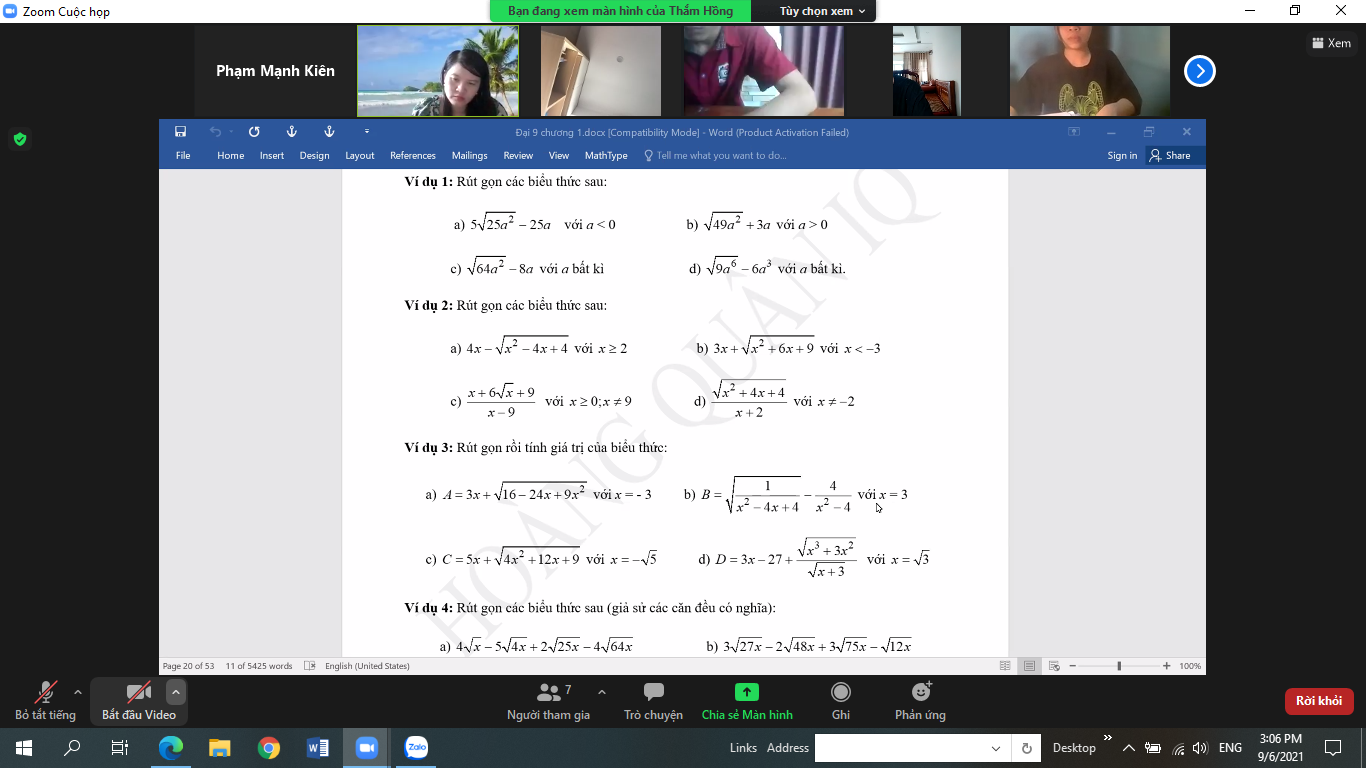
\(a,=\sqrt[3]{\left(x-1\right)^3}-\sqrt[3]{\left(5x+1\right)^3}=x-1-5x-1=-4x-2\\ b,=6a-6a+20a=20a\)
Bài 2:
\(a,=2\sqrt[3]{6}+3\sqrt[3]{5}-4\sqrt[3]{6}-2\sqrt[3]{5}=\sqrt[3]{5}-2\sqrt[3]{6}\\ b,=\sqrt[3]{8}-4\sqrt[3]{27}+2\sqrt[3]{64}=2-12+16=6\\ c,=\sqrt[3]{64}+\sqrt[3]{48}+\sqrt[3]{36}-\sqrt[3]{48}-\sqrt[3]{36}-\sqrt[3]{27}=4-3=1\\ d,=\sqrt[3]{162\left(-2\right)\cdot\dfrac{2}{3}}=\sqrt[3]{-216}=-6\)
PM
1
PM
1
19 tháng 10 2021
Bài 3:
a: Ta có: \(C=\dfrac{a^2+\sqrt{a}}{a-\sqrt{a}+1}-\dfrac{2a+\sqrt{a}}{\sqrt{a}}+1\)
\(=a+\sqrt{a}-2\sqrt{a}-1+1\)
\(=a-\sqrt{a}\)
b: Để C=2 thì \(\sqrt{a}-2=0\)
hay a=4
PM
1
6 tháng 10 2021
\(4,\\ a,ĐK:x>0;x\ne4;x\ne9\\ B=\dfrac{x+4\sqrt{x}+4-x+4\sqrt{x}-4+4x}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\cdot\dfrac{\sqrt{x}\left(2-\sqrt{x}\right)}{\sqrt{x}-3}\\ B=\dfrac{4\sqrt{x}\left(\sqrt{x}+2\right)}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\cdot\dfrac{\sqrt{x}\left(2-\sqrt{x}\right)}{\sqrt{x}-3}\\ B=\dfrac{4x}{\sqrt{x}-3}\)
\(b,B=1\Leftrightarrow4x=\sqrt{x}-3\Leftrightarrow4x-\sqrt{x}+3=0\\ \Leftrightarrow\left(4x-2\cdot2\cdot\dfrac{1}{4}\sqrt{x}+\dfrac{1}{16}\right)+\dfrac{47}{16}=0\\ \Leftrightarrow\left(2\sqrt{x}-\dfrac{1}{4}\right)^2+\dfrac{47}{16}=0\\ \Leftrightarrow x\in\varnothing\)
9 tháng 9 2021
\(3,\\ a,\dfrac{\left(1+\sqrt{x}\right)^2-4\sqrt{x}}{1-\sqrt{x}}\\ =\dfrac{\sqrt{x}-2\sqrt{x}+1}{1-\sqrt{x}}=\dfrac{\left(1-\sqrt{x}\right)^2}{1-\sqrt{x}}=1-\sqrt{x}=1-\sqrt{2}\)
\(b,\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+4\sqrt{xy}}{1+\sqrt{xy}}\\ =\dfrac{x+2\sqrt{xy}+y}{1+\sqrt{xy}}=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{1+\sqrt{xy}}\\ =\dfrac{\left(\sqrt{2}+\sqrt{3}\right)^2}{1+\sqrt{6}}=\dfrac{5+2\sqrt{6}}{1+\sqrt{6}}\\ =\dfrac{\left(5+2\sqrt{6}\right)\left(\sqrt{6}-1\right)}{5}\\ =\dfrac{3\sqrt{6}+7}{5}\)
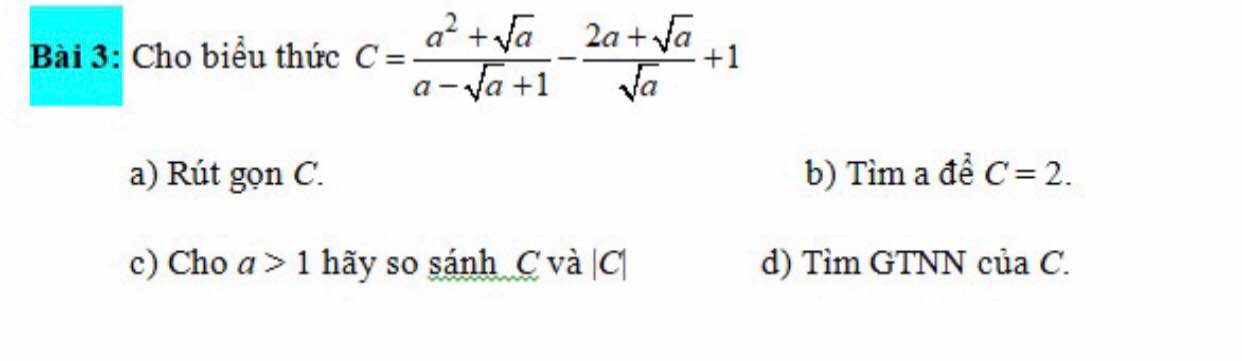
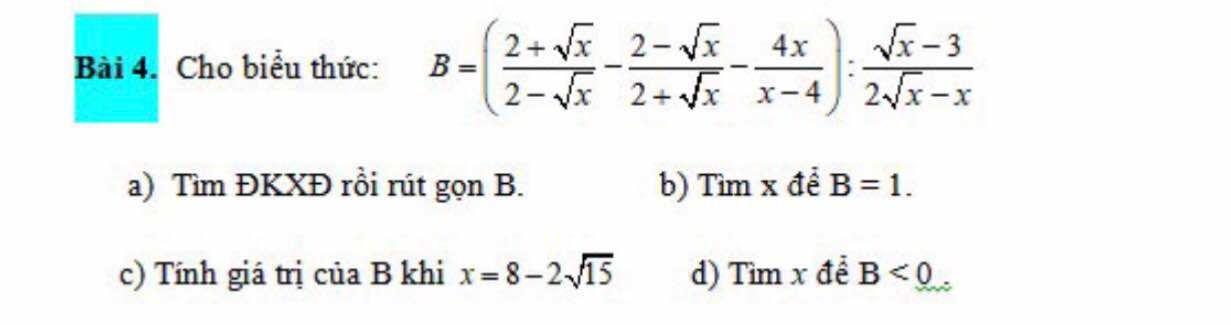
ta có
\(\left\{{}\begin{matrix}x+my=2\\mx-2y=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{m+4}{m^2+2}\\y=\dfrac{2m-1}{m^2+2}\end{matrix}\right.\)
để x>0 =>m+4>0 => m>-4
để y<0 => 2m-1<0 => m<1/2
=.> -4<m<1/2