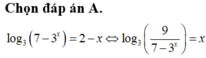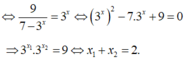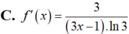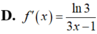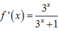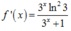K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên
A
0


PT
1
L
1

AH
Akai Haruma
Giáo viên
25 tháng 7 2017
Lời giải:
Để hàm số xác định với mọi \(x\in\mathbb{R}\) thì \(x^2-2(m+1)x+9>0\) với mọi số thực $x$
Áp dụng định lý về dấu của tam thức bậc 2, để thu được điều trên cần có:
\(\Delta'=(m+1)^2-9<0\)
\(\Leftrightarrow (m+4)(m-2)<0\Leftrightarrow -4< m<2\)

CM
14 tháng 2 2017
Chọn D.
Phương trình 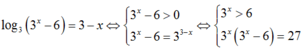
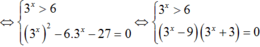
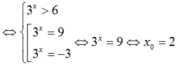
Mà x0 là nghiệm của phương trình log3( x + 7a) = 2log2x nên suy ra
log3( x + 7a) = 2log2x tương đương log3( x +7a) = 2
do đó; 7a + 2 = 32
suy ra a = 1.