Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(A=\left[\dfrac{x+3}{\left(x-3\right)^2}+\dfrac{6}{x^2-9}-\dfrac{x-3}{\left(x+3\right)^2}\right]\left[1:\left(\dfrac{24x^2}{x^4-81}-\dfrac{12}{x^2+9}\right)\right]\)
\(\left(ĐKXĐ:x\ne\pm3\right)\)
\(=\dfrac{\left(x+3\right)^3+6\left(x-3\right)\left(x+3\right)-\left(x-3\right)^3}{\left(x-3\right)^2\left(x+3\right)^2}\cdot\left[1:\dfrac{24x^2-12\left(x^2-9\right)}{\left(x^2-9\right)\left(x^2+9\right)}\right]\)
\(=\dfrac{x^3+9x^2+27x+27+6x^2-54-x^3+9x^2-27x+27}{\left(x-3\right)^2\left(x+3\right)^2}\cdot\dfrac{\left(x^2-9\right)\left(x^2+9\right)}{24x^2-12x^2+108}\)
\(=\dfrac{24x^2\left(x^2+9\right)\left(x-3\right)\left(x+3\right)}{12\left(x^2+9\right)\left(x-3\right)^2\left(x+3\right)^2}\)
\(=\dfrac{2x^2}{x^2-9}\)
b) \(B=\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right):\left[\left(x-2\right)+\dfrac{10-x^2}{x+2}\right]\)
\(=\left(\dfrac{x}{x^2-4}-\dfrac{2}{x-2}+\dfrac{1}{x+2}\right):\left(\dfrac{x-2}{1}+\dfrac{10-x^2}{x+2}\right)\)
\(=\dfrac{x-2\left(x+2\right)+x-2}{\left(x-2\right)\left(x+2\right)}:\dfrac{\left(x-2\right)\left(x+2\right)+10-x^2}{x+2}\)
\(=\dfrac{x-2x-4+x-2}{x^2-4}\cdot\dfrac{x+2}{x^2-4+10-x^2}\)
\(=\dfrac{-6\left(x+2\right)}{6\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{-1}{x-2}\)
phần b điều kiện xác định là \(x\ne\pm2\) nhé

1: =>3x+1=4
=>3x=3
hay x=1
2: \(\Leftrightarrow172\cdot x^2=\dfrac{1}{2^3}+\dfrac{7^9}{98^3}=\dfrac{1}{2^3}+\dfrac{7^9}{7^6\cdot2^3}\)
\(\Leftrightarrow172\cdot x^2=\dfrac{1}{2^3}+\dfrac{7^3}{2^3}=\dfrac{344}{2^3}\)
\(\Leftrightarrow x^2=\dfrac{1}{4}\)
=>x=1/2 hoặc x=-1/2
3: \(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{2}{9}=\dfrac{4}{9}\\x-\dfrac{2}{9}=-\dfrac{4}{9}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{2}{9}\end{matrix}\right.\)
4: =>x+2=0 và y-1/10=0
=>x=-2 và y=1/10

\(P=\left[\dfrac{x^2}{2x-9}\left(\dfrac{3}{x}-\dfrac{1}{x-3}\right)-\dfrac{x+6}{2\left(x-3\right)}\right]:\dfrac{x+2}{2\left(x-3\right)}\)
\(\Leftrightarrow P=\left[\dfrac{x^2}{2x-9}\left(\dfrac{3\left(x-3\right)}{x\left(x-3\right)}-\dfrac{x}{x\left(x-3\right)}\right)-\dfrac{x+6}{2\left(x-3\right)}\right]:\dfrac{x+2}{2\left(x-3\right)}\)
\(\Leftrightarrow P=\left[\dfrac{x^2}{2x-9}.\dfrac{3x-9-x}{x\left(x-3\right)}-\dfrac{x+6}{2\left(x-3\right)}\right]:\dfrac{x+2}{2\left(x-3\right)}\)
\(\Leftrightarrow P=\left[\dfrac{x^2}{2x-9}.\dfrac{2x-9}{x\left(x-3\right)}-\dfrac{x+6}{2\left(x-3\right)}\right]:\dfrac{x+2}{2\left(x-3\right)}\)
\(\Leftrightarrow P=\left[\dfrac{x^2.\left(2x-9\right)}{\left(2x-9\right)x\left(x-3\right)}-\dfrac{x+6}{2\left(x-3\right)}\right]:\dfrac{x+2}{2\left(x-3\right)}\)
\(\Leftrightarrow P=\left[\dfrac{x}{x-3}-\dfrac{x+6}{2\left(x-3\right)}\right]:\dfrac{x+2}{2\left(x-3\right)}\)
\(\Leftrightarrow P=\left[\dfrac{2x}{2\left(x-3\right)}-\dfrac{x+6}{2\left(x-3\right)}\right]:\dfrac{x+2}{2\left(x-3\right)}\)
\(\Leftrightarrow P=\dfrac{2x-\left(x+6\right)}{2\left(x-3\right)}:\dfrac{x+2}{2\left(x-3\right)}\)
\(\Leftrightarrow P=\dfrac{2x-x-6}{2\left(x-3\right)}:\dfrac{x+2}{2\left(x-3\right)}\)
\(\Leftrightarrow P=\dfrac{x-6}{2\left(x-3\right)}:\dfrac{x+2}{2\left(x-3\right)}\)
\(\Leftrightarrow P=\dfrac{x-6}{2\left(x-3\right)}.\dfrac{2\left(x-3\right)}{x+2}\)
\(\Leftrightarrow P=\dfrac{\left(x-6\right).2\left(x-3\right)}{2\left(x-3\right).\left(x+2\right)}\)
\(\Leftrightarrow P=\dfrac{x-6}{x+2}\)

b: Đặt \(x^2-6x-2=a\)
Theo đề, ta có: \(a+\dfrac{14}{a+9}=0\)
=>(a+2)(a+7)=0
\(\Leftrightarrow\left(x^2-6x\right)\left(x^2-6x+5\right)=0\)
=>x(x-6)(x-1)(x-5)=0
hay \(x\in\left\{0;1;6;5\right\}\)
c: \(\Leftrightarrow\dfrac{-8x^2}{3\left(2x-1\right)\left(2x+1\right)}=\dfrac{2x}{3\left(2x-1\right)}-\dfrac{8x+1}{4\left(2x+1\right)}\)
\(\Leftrightarrow-32x^2=8x\left(2x+1\right)-3\left(8x+1\right)\left(2x-1\right)\)
\(\Leftrightarrow-32x^2=16x^2+8x-3\left(16x^2-8x+2x-1\right)\)
\(\Leftrightarrow-48x^2=8x-48x^2+18x+3\)
=>26x=-3
hay x=-3/26

a: \(=-\dfrac{1}{x\left(x-1\right)}+\dfrac{-1}{\left(x-1\right)\left(x-2\right)}+\dfrac{-1}{\left(x-2\right)\left(x-3\right)}+...+-\dfrac{1}{\left(x-4\right)\left(x-5\right)}+\dfrac{1}{x-5}\)
\(=\dfrac{1}{x}-\dfrac{1}{x-1}+\dfrac{1}{x-1}-\dfrac{1}{x-2}+\dfrac{1}{x-2}-\dfrac{1}{x-3}+...+\dfrac{1}{x-4}-\dfrac{1}{x-5}+\dfrac{1}{x-5}\)
=1/x
b: \(=\dfrac{1}{x}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+6}+\dfrac{1}{x+6}-\dfrac{1}{x+9}+\dfrac{1}{x+9}\)
=1/x

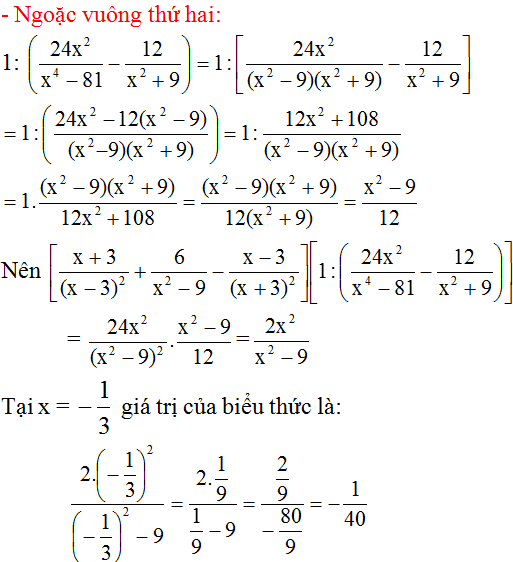


Bạn ơi mik ra \(\dfrac{x^3+45x-54}{12\left(x-3\right)\left(x+3\right)}\) có đúng không bạn?
Mình rút chx hết bạn bạn gửi cách làm bạn qua mình tham khảo đc k ạ?