làm xhi tiết lảm cả 2 bài chi tiết ạ

Khách

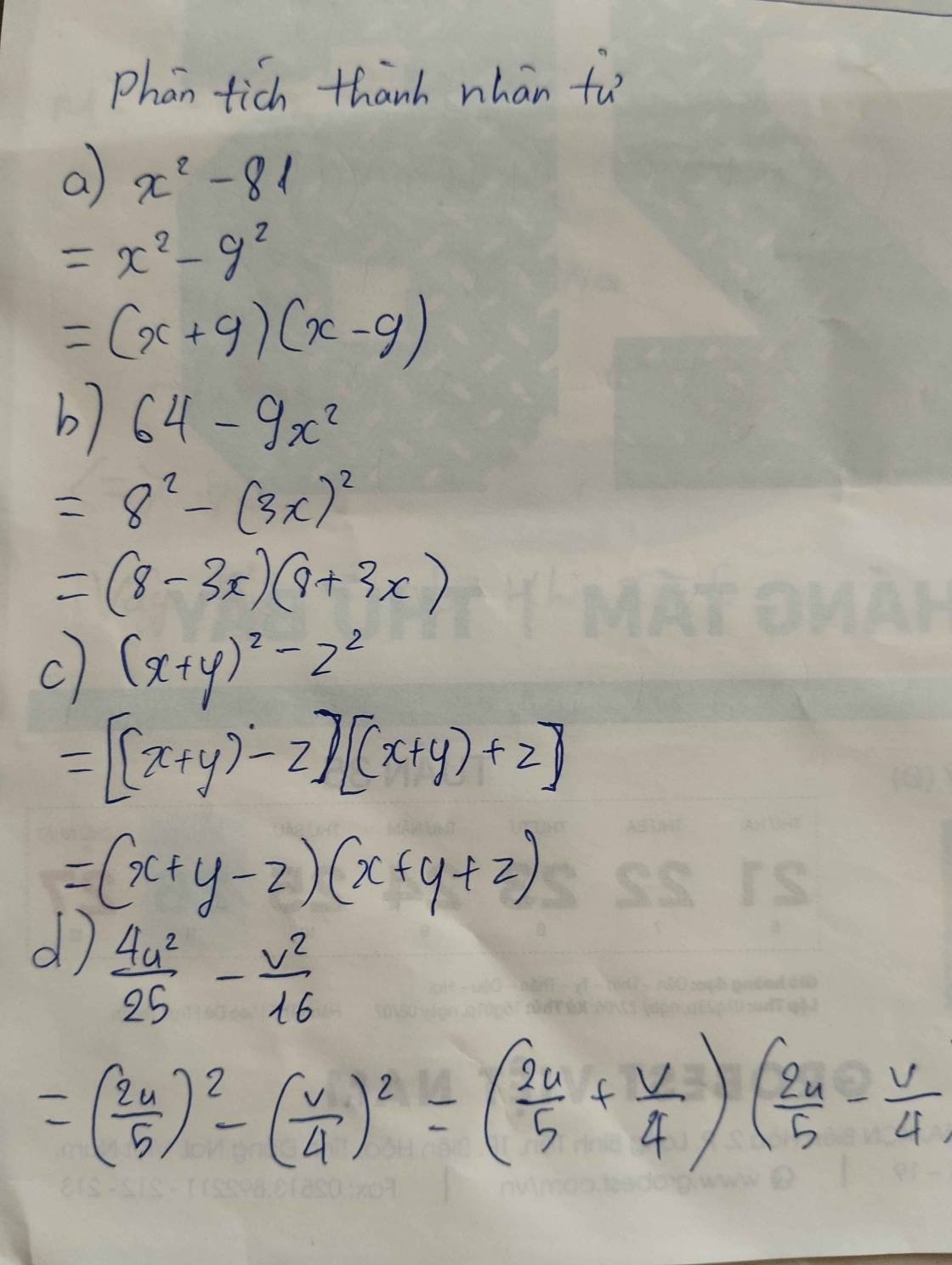
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Hà Thu

30 tháng 9 2023

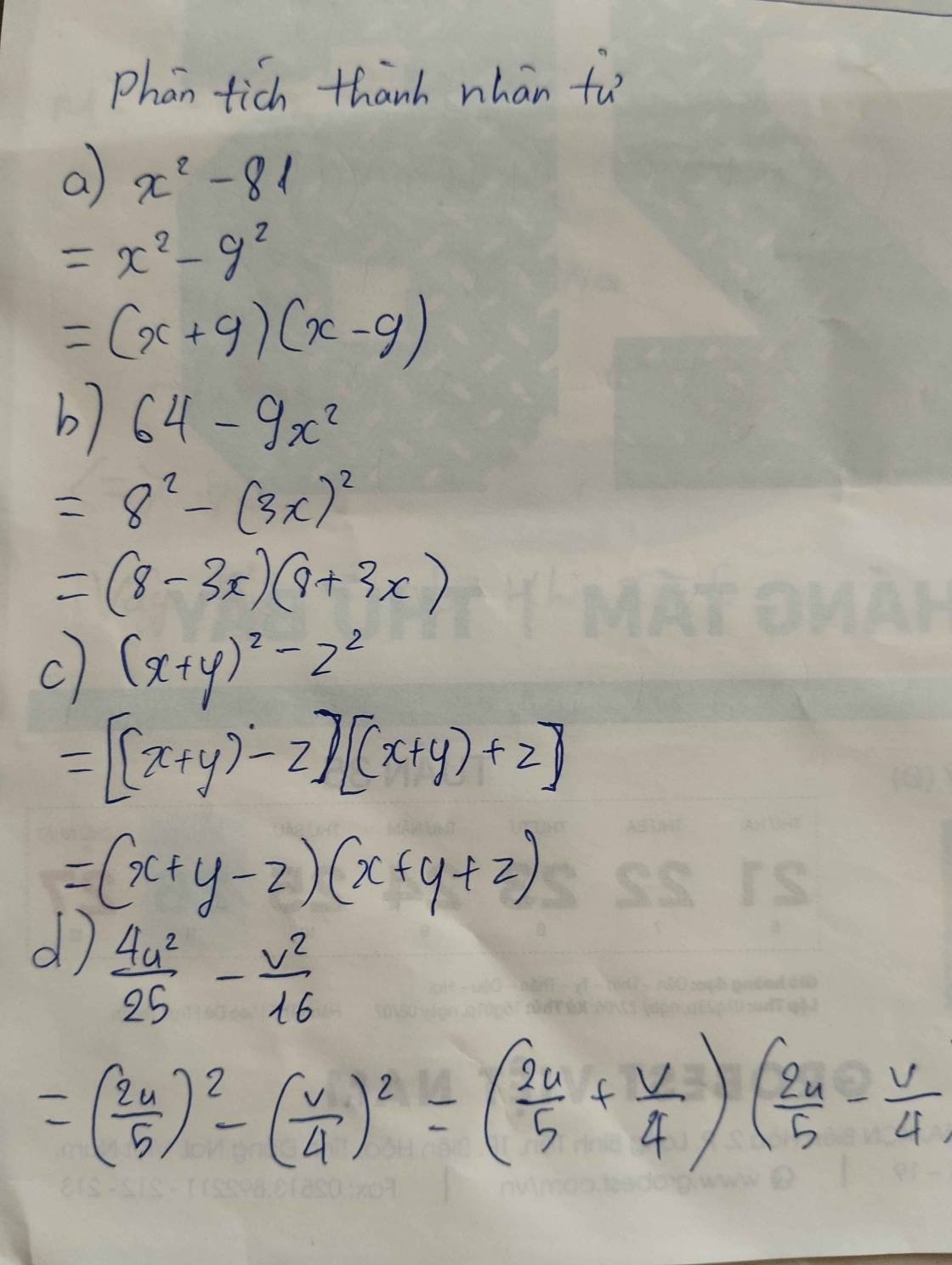
làm xhi tiết loading... lảm cả 2 bài chi tiết ạ

#Toán lớp 8

HT.Phong (9A5)

CTVHS

30 tháng 9 2023

Đúng(0)

HT.Phong (9A5)

CTVHS

30 tháng 9 2023

Đúng(1)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Hà Thu

18 tháng 11 2023

Làm bài 7 chi tiết ạ cả 2 càng tốt ạ

#Toán lớp 8

HT.Phong (9A5)

CTVHS

18 tháng 11 2023

Bài 8:

a) \(x^2-25x=0\)

\(\Leftrightarrow x\left(x-25\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-25=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=25\end{matrix}\right.\)

b) \(7x\left(x-3\right)-5\left(3-x\right)=0\)

\(\Leftrightarrow7x\left(x-3\right)+5\left(x-3\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(7x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\7x+5=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{7}\end{matrix}\right.\)

c) \(7x\left(x+4\right)-7x-28=0\)

\(\Leftrightarrow7x\left(x+4\right)-7\left(x+4\right)=0\)

\(\Leftrightarrow7\left(x+4\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x-1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=1\end{matrix}\right.\)

d) \(\left(2x^2+5x\right)\left(x^2-x\right)+\left(2x^2+10\right)\left(x-x^2\right)=0\)

\(\Leftrightarrow\left(2x^2+5x\right)\left(x^2-x\right)-\left(2x^2+10\right)\left(x^2-x\right)=0\)

\(\Leftrightarrow\left(x^2-x\right)\left(2x^2+5x-2x^2-10\right)=0\)

\(\Leftrightarrow x\left(x-1\right)\left(5x-10\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\\5x-10=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)

Đúng(2)

Nguyễn Lê Phước Thịnh

18 tháng 11 2023

a: \(4a^3b-12a^2b^2+8ab^3\)

\(=4ab\cdot a^2-4ab\cdot3ab+4ab\cdot2b^2\)

\(=4ab\left(a^2-3ab+2b^2\right)\)

\(=4ab\left(a^2-ab-2ab+2b^2\right)\)

\(=4ab\left[a\left(a-b\right)-2b\left(a-b\right)\right]\)

\(=4ab\left(a-b\right)\left(a-2b\right)\)

b: \(\dfrac{5}{2}x^4+\dfrac{3}{4}x^3-\dfrac{1}{5}x^2\)

\(=x^2\cdot\dfrac{5}{2}x^2+x^2\cdot\dfrac{3}{4}x-x^2\cdot\dfrac{1}{5}\)

\(=x^2\left(\dfrac{5}{2}x^2+\dfrac{3}{4}x-\dfrac{1}{5}\right)\)

c: \(3x^2\left(x+9\right)-2\left(x+9\right)\)

\(=\left(x+9\right)\cdot3x^2-\left(x+9\right)\cdot2\)

\(=\left(x+9\right)\left(3x^2-2\right)\)

d: \(3x^2\left(7x+y\right)-5x\left(7x+y\right)+14x+2y\)

\(=\left(7x+y\right)\left(3x^2-5x\right)+2\left(7x+y\right)\)

\(=\left(7x+y\right)\left(3x^2-5x+2\right)\)

\(=\left(7x+y\right)\left(3x^2-3x-2x+2\right)\)

\(=\left(7x+y\right)\left[3x\left(x-1\right)-2\left(x-1\right)\right]\)

\(=\left(7x+y\right)\left(x-1\right)\left(3x-2\right)\)

Đúng(1)

Hà Thu

12 tháng 1

Chi tiết em nới học nên làm chi tiết nhất ạ đề bài rút gọn phân thức

#Toán lớp 8

Nguyễn Việt Lâm

Giáo viên

12 tháng 1

\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)

\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)

Đúng(3)

Toru

12 tháng 1

d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)

Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)

e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)

Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)

Đúng(1)

Hà Thu

26 tháng 8 2023

Làm bài 4 chi tiết ạ

#Toán lớp 8

Nguyễn Lê Phước Thịnh

26 tháng 8 2023

a: \(=5x^2y^2\cdot\dfrac{7}{10}x^4y\cdot40x^2z^3\)

\(=\left(5\cdot\dfrac{7}{10}\cdot40\right)\left(x^2y^2\cdot x^4y\cdot x^2z^3\right)\)

\(=140x^8y^3z^3\)

Bậc là 8+3+3=14

b: \(=-\dfrac{1}{2}\cdot ab\cdot\dfrac{-4}{3}\cdot a^2bc\cdot5c^2b^3\)

\(=\left(\dfrac{1}{2}\cdot\dfrac{4}{3}\cdot5\right)\cdot ab\cdot a^2b\cdot c\cdot c^2b^3\)

\(=\dfrac{10}{3}a^3b^5c^3\)

Bậc là 11

c: \(=-1.2\cdot ab\cdot100a^4b^2\cdot c^3\cdot\left(-1.5\right)\cdot a^2c\)

\(=1.8\cdot100\cdot ab\cdot a^4b^2c^3\cdot a^2c\)

\(=180a^7b^3c^4\)

Bậc là 14

Đúng(3)

Hà Thu

18 tháng 11 2023

Làm bài 12 giúp ạ chi tiết

#Toán lớp 8

HT.Phong (9A5)

CTVHS

18 tháng 11 2023

Bài 12:

a) \(4x^2+4x+1=0\)

\(\Leftrightarrow\left(2x\right)^2+2\cdot2x\cdot1+1^2=0\)

\(\Leftrightarrow\left(2x+1\right)^2=0\)

\(\Leftrightarrow2x+1=0\)

\(\Leftrightarrow x=-\dfrac{1}{2}\)

b) \(x^2-2x=-1\)

\(\Leftrightarrow x^2-2x+1=0\)

\(\Leftrightarrow\left(x-1\right)^2=0\)

\(\Leftrightarrow x-1=0\)

\(\Leftrightarrow x=1\)

c) \(-x^2+10x=25\)

\(\Leftrightarrow-x^2+10x-25=0\)

\(\Leftrightarrow-\left(x^2-10x+25\right)=0\)

\(\Leftrightarrow-\left(x-5\right)^2=0\)

\(\Leftrightarrow x-5=0\)

\(\Leftrightarrow x=5\)

d) \(9=12x-4x^2\)

\(\Leftrightarrow4x^2-12x+9=0\)

\(\Leftrightarrow\left(2x-3\right)^2=0\)

\(\Leftrightarrow2x-3=0\)

\(\Leftrightarrow2x=3\)

\(\Leftrightarrow x=\dfrac{3}{2}\)

Đúng(1)

Tiến Đạt Inuyasha

8 tháng 4 2018 - olm

giải bài toán bằng cách lập pt

trong tháng đầu cả hai tổ công nhân làm được 800 chi tiết máy. Tháng thứ 2,tổ 1 vượt mưc cho phép là 15% ,tổ 2 làm vượt mưc cho phép là 20%,do đó cả 2 tổ sản xuất được 945 chi tiết máy. Tính xem trong tháng đầu mỗi tổ sản xuất đươc bao nhiêu chi tiết máy?

#Toán lớp 8