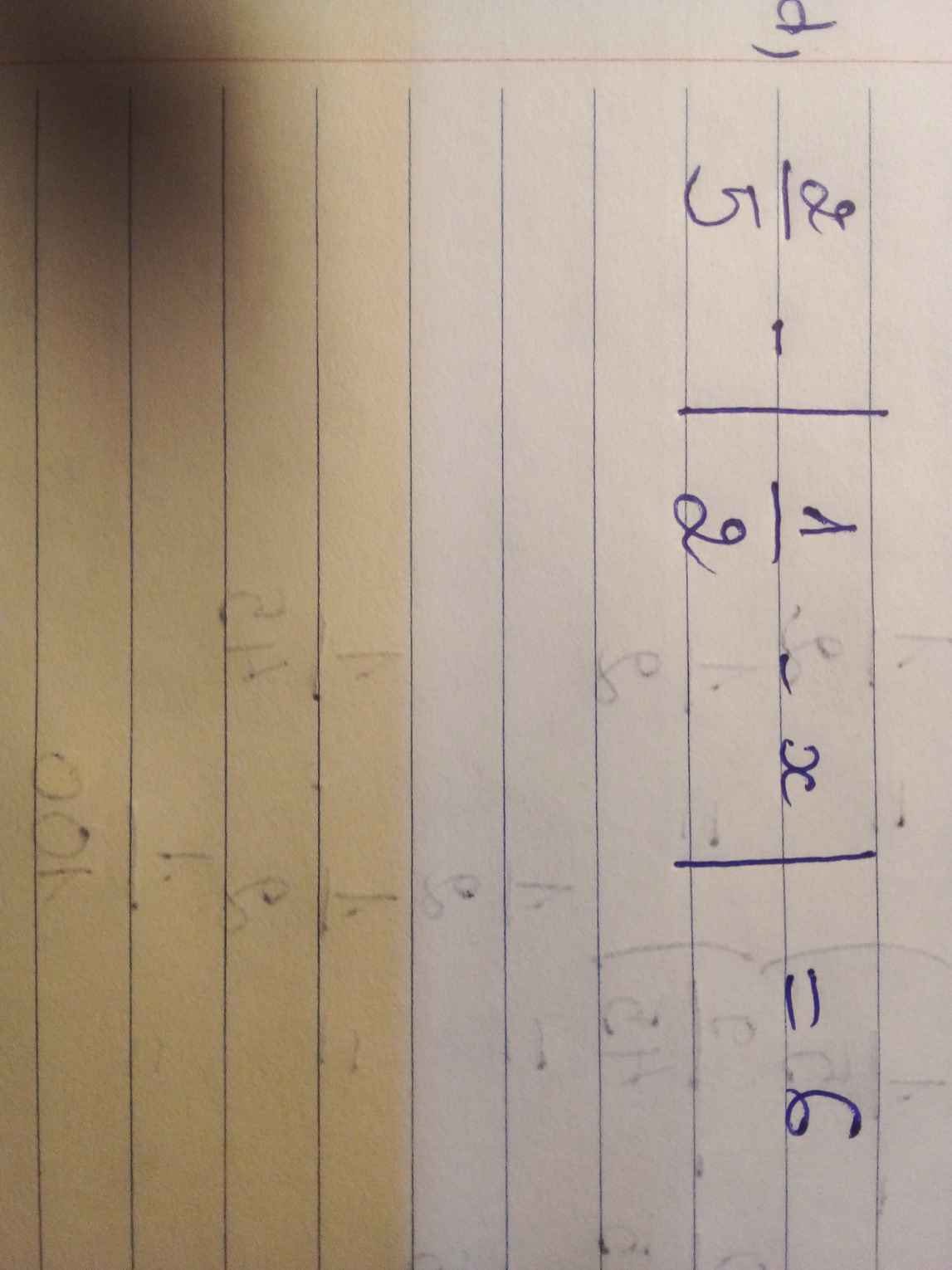Làm ngay bây giờ cho mk vs, mk cần gấp lắm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
A
11 tháng 2 2018
Gọi S có n số hạng sao cho S = 1+ 2+ 3 + ...+ n = aaa ( a là chữ số)
\(\Rightarrow\)(n + 1).n : 2 = a.111
\(\Rightarrow\) n(n + 1) = a.222
\(\Rightarrow\) n(n + 1) = a.2.3.37
a là chữ số mà n; n + 1 là hai số tự nhiên liên tiếp nên a = 6
\(\Rightarrow\)n(n + 1) = 36.37 \(\Rightarrow\) n = 36
Vậy cần 36 số hạng.
TQ
1
5 tháng 2 2022
3xy + y=4-x
<=>9xy+3y=12-3x
<=>9xy+3y+3x+1=13
<=>3y.(3x+1)+(3x+1)=13
<=>(3x+1)(3y+1)=13
<=> *{3x+1=13y+1=13{3x+1=13y+1=13<=>{x=0y=4{x=0y=4(nhận)
*{3x+1=123y+1=1{3x+1=123y+1=1<=>{x=4y=0{x=4y=0(nhận)
*{3x+1=−13y+1=−13{3x+1=−13y+1=−13<=>{x=−23y=−143{x=−23y=−143(loại)
*{3x+1=−133y+1=−1{3x+1=−133y+1=−1<=>{x=−143y=−23{x=−143y=−23(loại)
Vậy x=4 thì y=0 ; x=0 thì y=4
HM
2
15 tháng 9 2021
\(\dfrac{2}{5}-\left|\dfrac{1}{2}-x\right|=6\)
\(\Leftrightarrow\left|\dfrac{1}{2}-x\right|=\dfrac{2}{5}-6\)
\(\Leftrightarrow\left|\dfrac{1}{2}-x\right|=-\dfrac{28}{5}\)( vô lý do \(\left|\dfrac{1}{2}-x\right|\ge0\forall x\))
Vậy \(x\in\left\{\varnothing\right\}\)
15 tháng 9 2021
\(\Rightarrow\left|\dfrac{1}{2}-x\right|=\dfrac{2}{5}-6=-\dfrac{28}{5}\\ \Rightarrow\left[{}\begin{matrix}\dfrac{1}{2}-x=-\dfrac{28}{5},\forall\dfrac{1}{2}-x\ge0\\\dfrac{1}{2}-x=\dfrac{28}{5},\forall\dfrac{1}{2}-x< 0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{61}{10},\forall x\le\dfrac{1}{2}\left(loại\right)\\x=-\dfrac{51}{10},\forall x>\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\Rightarrow x\in\varnothing\)
??????????????
TM
0
