
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3. Xét tam giác ADM và tam giác AEM có :
góc ADM = góc AEM = 90 độ
Góc BAM = góc CAM (gt)
AM chung
=>Tam giác ADM = tam giác AEm (c.huyền - g.nhọn)
=>MD = ME (cặp cạnh t/ứng )
AD = AE (cặp cạnh t/ứng )
Xét tam giác MDB và tam giác MEC có :
MB = MC (gt)
góc MDB = góc MEC = 90 độ
MD = ME ( câu a)
=>Tam giác MDB = Tam giác MEC (c.huyền-c.g.vuông)
Vì AD + DB = AB
AE + EC = AC
Mà AD = AE
DB = EC
=>AB = AC
Xét tam giác ABM và tam giác ACM có
AM chung
góc BAM = góc CAM (gt)
AB = AC (CMT)
=>Tam giác ABM = Tam giác ACM (c.huyền-g.nhon)
Vậy có 3 cặp tam giác bằng nhau

Câu hỏi của Nguyễn Trọng Phúc - Toán lớp 7 | Học trực tuyến

\(\left(x-3\right).\left(x-2015\right)< 0\)
\(\Rightarrow\left(x-3\right)và\left(x-2015\right)\) phải khác dấu
\(\Rightarrow\left(x-3\right)< \left(x-2015\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x-3>0\\x-2015< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>3\\x< 2015\end{matrix}\right.\)
\(\Rightarrow3< x< 2015\)
\(\Rightarrow x\in\left\{4;5;6;7;8;...;2013;2014\right\}\)
( ko bt đúng hay sai nx )
thám tử
\(\left(x-3\right)\left(x-2015\right)< 0\)
Với mọi \(x\in R\) thì:
\(x-2015< x-3\)
Khi đó: \(\left\{{}\begin{matrix}x-2015< 0\\x-3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 2015\\x>3\end{matrix}\right.\)
Nên \(3< x< 2015\)

Này phạm nhất duy , chắc có lẽ bạn chưa học , nếu \(\Delta\)ABD cân ( vì AD = AB ) mà AK là đường phân giác của tam giác đó thì \(\Rightarrow\) AK là đường cao , đường trung tuyến , đường trung trực của \(\Delta\)ABD

\(\left|x-\dfrac{1}{2}\right|+\left|y+\dfrac{2}{3}\right|+\left|x^2+xz\right|=0\)
\(\left\{{}\begin{matrix}\left|x-\dfrac{1}{2}\right|\ge0\forall x\\\left|y+\dfrac{2}{3}\right|\ge0\forall y\\\left|x^2+xz\right|\ge0\forall x;z\end{matrix}\right.\) \(\Rightarrow\left|x-\dfrac{1}{2}\right|+\left|y+\dfrac{2}{3}\right|+\left|x^2+xz\right|\ge0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\left|x-\dfrac{1}{2}\right|=0\\\left|y+\dfrac{2}{3}\right|=0\\\left|x^2+xz\right|=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-\dfrac{2}{3}\\z=-\dfrac{1}{2}\end{matrix}\right.\)

\(\left(x-3\right)^2+\left|y^2-9\right|=0\)
Vì \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge0\forall x\\\left|y^2-9\right|\ge0\forall y\end{matrix}\right.\)
để bt = 0 \(\Leftrightarrow\left\{{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\y^2-9=0\Rightarrow y^2=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)
Vậy.....
\(\left(x-3\right)^2+\left|y^2-9\right|=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\y^2-9=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\y^2=9\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=3\\y=3hoặcy=-3\end{matrix}\right.\)
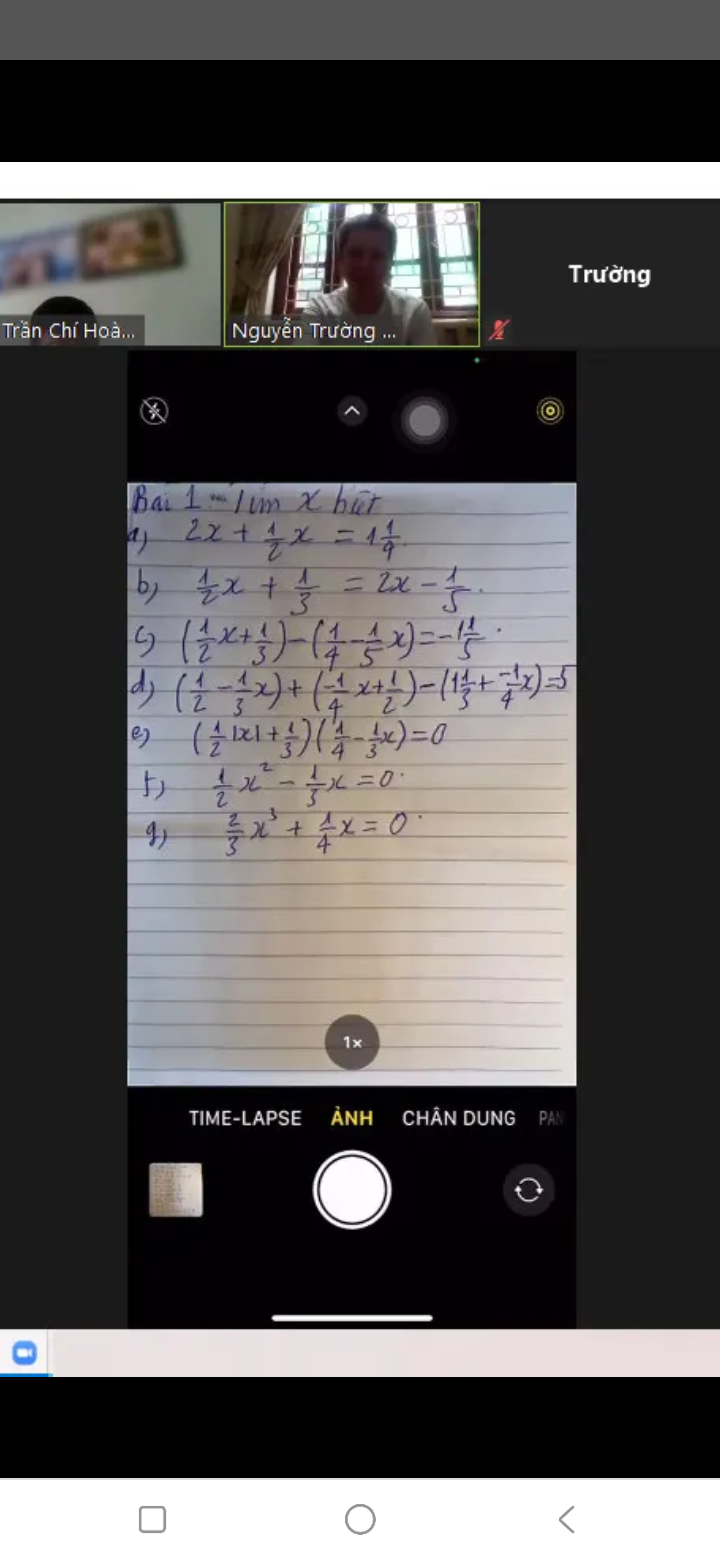

 M.n giải hộ em vs đg cần gấp ạ
M.n giải hộ em vs đg cần gấp ạ

