
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1)
a) 4y2-4xy+x2= x2-4xy+4y2= (x-2y)2
b) 9x2-12xy+4y2= (3x)2-2.3x.2y+(2y)2= (3x-2y)2
c) 16x2-25=(4x)2-52= (4x-5)(4x+5)
d) 1-9y2= 12-(3y)2=(1-3y)(1+3y)
g) x3-27y3= (x-3y)(x2+3xy+9y2)
h) 64 + 8x3=(4+2x)(16+8x+4x2)

Bài 5:
e: \(\dfrac{2}{x+1}=\dfrac{2x^2-2x+2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(\dfrac{3}{x^2-x+1}=\dfrac{3x+3}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(2,\\ a,=2x^2+4x-3x-6-2x^2-4x-2=-3x-8\\ b,=\left[x-2+2\left(x+1\right)\right]^2=\left(x-2+2x+2\right)^2=9x^2\)

Bài 1:
a: =8xy/2x=4y
b: \(=\dfrac{4x-1-7x+1}{3x^2y}=\dfrac{-3x}{3x^2y}=\dfrac{-1}{xy}\)
c: \(=\dfrac{3x-x+6}{2x\left(x+3\right)}=\dfrac{2\left(x+3\right)}{2x\left(x+3\right)}=\dfrac{1}{x}\)
e: \(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}=\dfrac{-10}{4}=-\dfrac{5}{2}\)


Bài 1 :
\(a,P=\dfrac{3x^2+3x}{\left(x+1\right)\left(2x-6\right)}\left(dkxd:x\ne-1;3\right)\)
\(=\dfrac{3x\left(x+1\right)}{\left(x+1\right)\left(2x-6\right)}\)
\(=\dfrac{3x}{2x-6}\)
Để P = 1 thì :
\(\dfrac{3x}{2x-6}=1\)
\(\Leftrightarrow\dfrac{3x-2x+6}{2x-6}=0\)
\(\Leftrightarrow x=-6\)

Bài 1:
a) \(\Leftrightarrow x^2-8x+16-x^2+4=6\\ \Leftrightarrow-8x=-14\\ \Leftrightarrow x=\dfrac{7}{4}\)
b) \(\Leftrightarrow\left(x^2-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)^2\left(x+1\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
c) \(\Leftrightarrow\left[{}\begin{matrix}3x-1=x+2\\3x-1=-x-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=3\\4x=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
Bài 2:
a) \(=5\left(x^2-2xy+y^2-4z^2\right)=5\left[\left(x-y\right)^2-\left(2z\right)^2\right]=5\left(x-y-2z\right)\left(x-y+2z\right)\)
b) \(=\left(x+1\right)^3-\left(3z\right)^3=\left(x-3z+1\right)\left[\left(x+1\right)^2+3z\left(x+1\right)+\left(3z\right)^2\right]=\left(x-3z+1\right)\left(x^2+2x+1+3xz+3z+9z^2\right)\)
c) \(=x\left(x^2-16\right)-15x\left(x-4\right)=x\left(x+4\right)\left(x-4\right)-15x\left(x-4\right)=\left(x-4\right)\left(x^2+4x-15x\right)=\left(x-4\right)\left(x^2-11x\right)=x\left(x-4\right)\left(x-11\right)\)

Bài 1:
b) \(B=A.\dfrac{-10}{x-4}=\dfrac{x-4}{x+5}.\dfrac{-10}{x-4}=\dfrac{-10}{x+5}\)
Để B nguyên <=> x+5 nguyên mà \(x\in Z\Rightarrow x+5\inƯ\left(-10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
\(\Leftrightarrow x\in\left\{-6;-4;-3;-7;0;-10;-15;5\right\}\) kết hợp với điều kiện của x
\(\Rightarrow x\in\left\{-15;-10;-6;-7;-3;0;5\right\}\)
Bài 5:
Có \(\left|x-2018\right|+\left|2x-2019\right|+\left|3x-2020\right|\ge0\) \(\forall\)x
\(\Rightarrow x-2021\ge0\) \(\Leftrightarrow x\ge2021\)
\(\Rightarrow x-2018>0,2x-2019>0,3x-2020>0\)
PT \(\Leftrightarrow x-2018+2x-2019+3x-2020=x-2021\)
\(\Leftrightarrow5x=4036\) \(\Leftrightarrow x=\dfrac{4036}{5}< 2021\) (L)
Vậy pt vô nghiệm






 Giúp em với ạ
Giúp em với ạ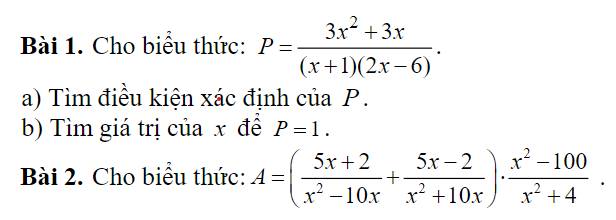


 Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!