Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
FN là tiếp tuyến tại N \(\Rightarrow\widehat{FNO}=90^0\)
\(\Rightarrow\) 2 điểm P và N cùng nhìn OF dưới 1 góc vuông nên tứ giác ONFP nội tiếp đường tròn đường kính ON
b.
Trong tam giác MQF, do \(PQ\perp ME\) và \(MN\perp FQ\Rightarrow O\) là trực tâm
\(\Rightarrow FO\perp MQ\) tại D
Hai điểm D và N cùng nhìn MF dưới 1 góc vuông
\(\Rightarrow DNFM\) nội tiếp
\(\Rightarrow\widehat{FDN}=\widehat{FMN}\) (cùng chắn FN) (1)
Hai điểm D và P cùng nhìn OM dưới 1 góc vuông
\(\Rightarrow MDOP\) nội tiếp
\(\Rightarrow\widehat{FMN}=\widehat{FDP}\) (cùng chắn OP) (2)
(1);(2) \(\Rightarrow\widehat{FDP}=\widehat{FDN}\)
\(\Rightarrow DF\) là phân giác của \(\widehat{PDN}\)
c.
Do MN là đường kính và E thuộc đường tròn \(\Rightarrow\widehat{MEN}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{MEN}=90^0\Rightarrow NE\perp ME\)
Áp dụng hệ thức lượng trong tam giác vuông MNF với đường cao NE:
\(MN^2=ME.MF\Rightarrow\left(2R\right)^2=ME.MF\)
\(\Rightarrow ME.MF=4R^2\)
Từ đó áp dụng BĐT Cô-si ta có:
\(MF+2ME\ge2\sqrt{MF.2ME}=2\sqrt{8R^2}=4R\sqrt{2}\)
Dấu "=" xảy ra khi \(MF=2ME\Rightarrow E\) là trung điểm MF
\(\Rightarrow NE\) là trung tuyến ứng với cạnh huyền
\(\Rightarrow NE=\dfrac{1}{2}MF=ME\)
\(\Rightarrow E\) là điểm chính giữa cung MN

Đề: Dẫn 17,92 lít khí hidro đi qua ống sứ m gam , 1 oxit sắt FexOy nung nóng sau phản ứng thu được 2,4*10^23 phân tử nước và hỗn hợp X gồm 2 chất rắng nặng 28.4 g

1.2 với \(x\ge0,x\in Z\)
A=\(\dfrac{2\sqrt{x}+7}{\sqrt{x}+2}=2+\dfrac{3}{\sqrt{x}+2}\in Z< =>\sqrt{x}+2\inƯ\left(3\right)=\left(\pm1;\pm3\right)\)
*\(\sqrt{x}+2=1=>\sqrt{x}=-1\)(vô lí)
*\(\sqrt{x}+2=-1=>\sqrt{x}=-3\)(vô lí
*\(\sqrt{x}+2=3=>x=1\)(TM)
*\(\sqrt{x}+2=-3=\sqrt{x}=-5\)(vô lí)
vậy x=1 thì A\(\in Z\)

3:
a: \(\Leftrightarrow x+1-6\sqrt{x+1}-9=0\)
=>\(\left(\sqrt{x+1}-3\right)=0\)
=>x+1=9
=>x=8
b: \(\Leftrightarrow\sqrt{\dfrac{1}{2}x-\dfrac{7}{4}\sqrt{\left(\sqrt{\dfrac{1}{2}x+1}+3\right)}}=10\)
=>\(\sqrt{\dfrac{1}{2}x-\dfrac{7}{4}\sqrt{\dfrac{1}{2}x+1}-\dfrac{21}{4}}=10\)
=>\(\dfrac{1}{2}x-\dfrac{21}{4}-\dfrac{7}{4}\sqrt{\dfrac{1}{2}x+1}=100\)
=>\(\dfrac{7}{4}\cdot\sqrt{\dfrac{1}{2}x+1}=\dfrac{1}{2}x-\dfrac{21}{4}-100=\dfrac{1}{2}x-\dfrac{421}{4}\)
=>\(\sqrt{\dfrac{1}{2}x+1}=\dfrac{2}{7}x-\dfrac{421}{7}\)
=>1/2x+1=(2/7x-421/7)^2
=>1/2x+1=4/49x^2-1684/49x+177241/49
=>\(x\simeq249,77;x\simeq177,36\)

k/ \(\sqrt{8+\sqrt{60}}-\sqrt{\dfrac{2}{\sqrt{15}+4}}=\sqrt{\left(\sqrt{3}+\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}=\sqrt{3}+\sqrt{5}-\sqrt{5}+\sqrt{3}=2\sqrt{3}\)
l/ \(\sqrt{\dfrac{3\sqrt{5}-1}{2\sqrt{5}+3}}=\sqrt{\dfrac{\left(3\sqrt{5}-1\right)\left(2\sqrt{5}-3\right)}{11}}=\sqrt{\dfrac{33-11\sqrt{5}}{11}}=\sqrt{3-\sqrt{5}}\)
\(\sqrt{\dfrac{\sqrt{5}+11}{7-2\sqrt{5}}}=\sqrt{\dfrac{\left(\sqrt{5}+11\right)\left(7+2\sqrt{5}\right)}{29}}=\sqrt{\dfrac{87+29\sqrt{5}}{29}}=\sqrt{3+\sqrt{5}}\)
\(\sqrt{\dfrac{3\sqrt{5}-1}{2\sqrt{5}+3}}-\sqrt{\dfrac{\sqrt{5}+11}{7-2\sqrt{5}}}=\sqrt{3-\sqrt{5}}-\sqrt{3+\sqrt{5}}=\dfrac{-2\sqrt{5}}{\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}}\)


Đề sai rồi vì `P>0AAx>=0,x ne 1/2` mà phải tìm để `P<=0` nên nhất thiết mẫu là `2sqrtx-1` mặt khác còn lý do nữa là `x ne 1/2` mà không phải là `1/4` nên mình vẫn băn khoăn nhưng lý do đầu có vẻ thuyết phục hơn và sửa lại là `x ne 1/4` nhé!
`|P|>=P`
Mà `|P|>=0`
`=>P<=0`
`<=>(sqrtx+2)/(2sqrtx-1)<=0`
Mà `sqrtx+2>=2>0AAx>=0`
`<=>2sqrtx-1<0`
`<=>2sqrtx<1`
`<=>sqrtx<1/2`
`<=>x<1/4`
Vậy với `0<=x<1/4` thì `|P|>=P.`


 giúp vs m đg cần gấp
giúp vs m đg cần gấp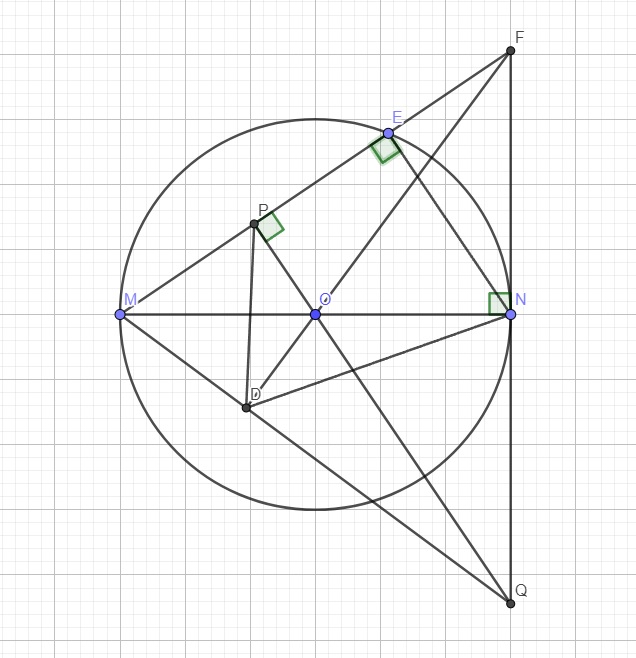

 Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với 




\(A=\dfrac{4x+2\sqrt{x}+2}{2\sqrt{x}+1}=\dfrac{2\sqrt{x}\left(2\sqrt{x}+1\right)+2}{2\sqrt{x}+1}=2\sqrt{x}+\dfrac{2}{2\sqrt{x}+1}\)
\(=2\sqrt{x}+1+\dfrac{2}{2\sqrt{x}+1}-1\ge2\sqrt{\left(2\sqrt{x}+1\right)\cdot\dfrac{2}{2\sqrt{x}+1}}-1=2\sqrt{2}-1\)
=> A \(\ge2\sqrt{2}-1\)
Dấu "=" xảy ra <=> \(2\sqrt{x}+1=\dfrac{2}{2\sqrt{x}+1}\)
<=> \(\left(2\sqrt{x}+1\right)^2=2\) <=> \(\left[{}\begin{matrix}2\sqrt{x}+1=2\\2\sqrt{x}+1=-2\left(loại\right)\end{matrix}\right.\)
<=> \(\sqrt{x}=\dfrac{1}{2}\) <=> \(x=\dfrac{1}{4}\)(tm)
Vậy minA = \(2\sqrt{2}-1\) khi x = 1/4