
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4:
h: -(x-9)(2x-1)
=-(2x^2-x-18x+9)
=-2x^2+19x-9
k: -(2x+3)(x-7)
=-(2x^2-14x+3x-21)
=-2x^2+11x+21
l: -(6x+1)(5x-9)
=-(30x^2-54x+5x-9)
=-30x^2+49x+9
m: =(2x-5)(7x-3)
=14x^2-6x-35x+15
=14x^2-41x+15
n: =(6x-8)(x-9)
=6x^2-54x-8x+72
=6x^2-62x+72
5:
a: \(=2x^3-2x^2+2x+3x^2-6x+24x-48-5x-5\)
=2x^3+x^2+15x-5
b: \(=4x^2+20x+2x^2+14x-6x-42-15x+27\)
=6x^2+13x-15
c: \(=-7x^2+14x+2x^2-4x+10x-20-3x^2+3x\)
=-8x^2+23x-20

c) Ta có \(\Delta AHB\sim\Delta ADC(g.g)\) nên \(\dfrac{BH}{BA}=\dfrac{CD}{CA}\).
Lại có \(\dfrac{BI}{BH}=\dfrac{CN}{CD}\) nên \(\dfrac{BI}{BA}=\dfrac{CN}{CA}\).
Mà \(\widehat{IBA}=\widehat{NCA}\) nên \(\Delta IBA\sim\Delta NCA(c.g.c)\)
\(\Rightarrow \widehat{ANC}=\widehat{AIB}\)
\(\Rightarrow\widehat{AID}=\widehat{AND}\).
Mà \(\widehat{API}=\widehat{DPN}\) (đối đỉnh) nên \(\Delta API\sim\Delta DPN(g.g)\)
\(\Rightarrow\dfrac{PA}{PI}=\dfrac{PD}{PN}\).
Mà \(\widehat{APD}=\widehat{IPN}\) (đối đỉnh) nên \(\Delta APD\sim\Delta IPN(c.g.c)\)
\(\Rightarrow\widehat{PIN}=\widehat{PAD}\).
Ta có \(\widehat{AIN}=\widehat{AID}+\widehat{NID}=\widehat{NAD}+\widehat{AND}=90^o\) nên \(AI\perp NI\).


Kẻ AP, CK, BQ vuông góc với xy (P, K, Q là chân đường vuông góc).
Hình thang APQB có : \(\hept{\begin{cases}AC=CB\\CK//AP//BQ\end{cases}}\)
=> KP = KQ (hình chiếu của hai đoạn thẳng bằng nhau)
=> CK là đường trung bình và cũng là khoảng cách từ trung điểm C của AB đến xy.
Do đó : \(CK=\frac{AP+BQ}{2}=\frac{12+20}{2}=6\left(cm\right)\)
Vậy khoảng cách từ trung điểm C của AB đến xy là CK=16(cm) .
Chúc bạn học tốt !!!

`a)P(x)+Q(x)=x^5-2x^2+1`
`=>Q(x)=x^5-2x^2+1-P(x)`
`=>Q(x)=x^5-2x^2+1-x^4+3x^2-1/2+x`
`=>Q(x)=x^5-x^4+x^2+x+1/2`
______________________________________________
`b)P(x)-R(x)=x^3`
`=>R(x)=P(x)-x^3`
`=>R(x)=x^4-3x^2+1/2-x-x^3`
`=>R(x)=x^4-x^3-3x^2-x+1/2`
Ta có:
\(P\left(x\right)+Q\left(x\right)=x^5-2x^2+1\)
\(\Rightarrow Q\left(x\right)=P\left(x\right)-\left(x^5-2x^2+1\right)\)
\(=x^4-3x^2+\dfrac{1}{2}-x-x^5+2x^2-1\)
\(=-x^5+x^4-x^2-x-\dfrac{1}{2}\)
Vậy \(Q\left(x\right)=-5^2+x^4-x^2-x-\dfrac{1}{2}\)

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: AH=DE
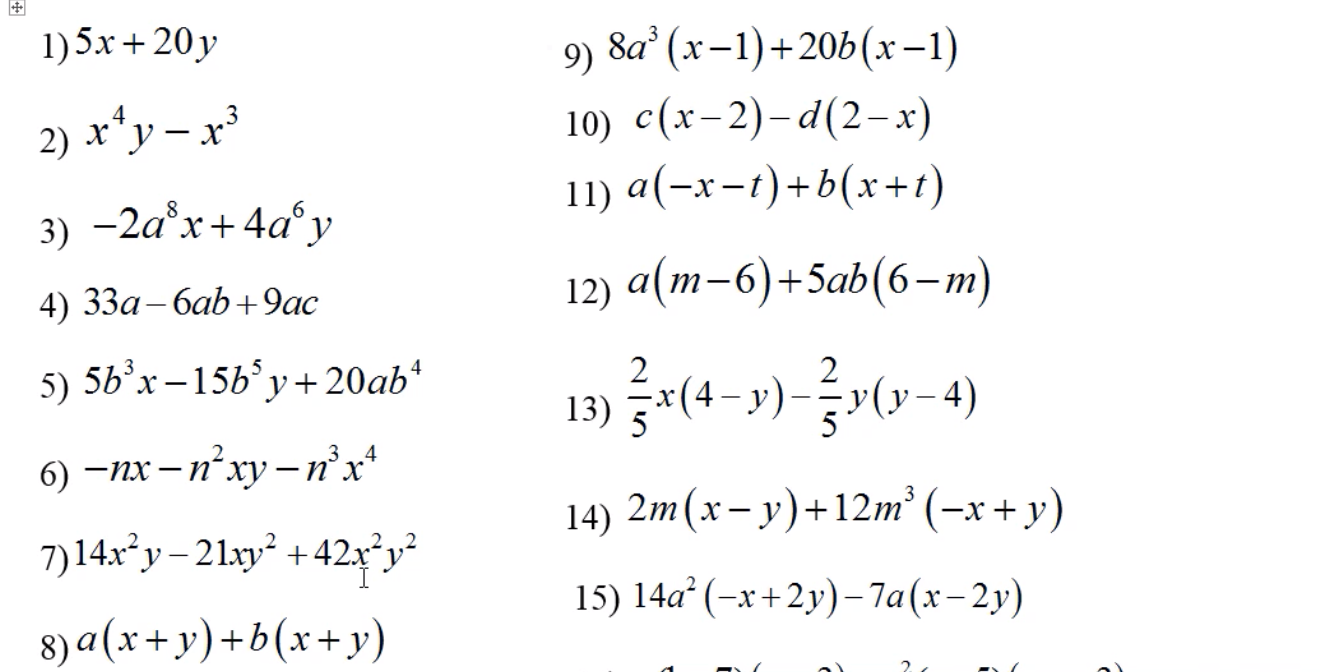



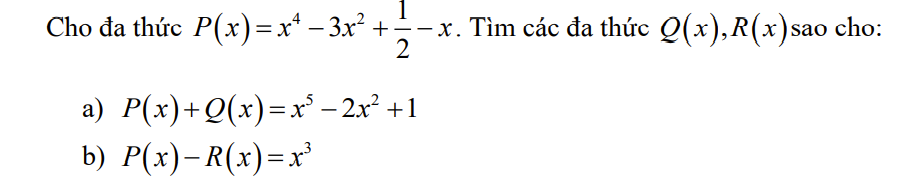

11.
$=-a(x+t)+b(x+t)=(x+t)(-a+b)=(b-a)(x+t)$
12.
$=a(m-6)-5ab(m-6)=a(m-6)(1-5b)$
13.
$=\frac{2}{5}x(4-y)+\frac{2}{5}y(4-y)$
$=\frac{2}{5}(4-y)(x+y)$
14.
$=2m(x-y)-12m^3(x-y)$
$=2m(x-y)(1-6m^2)$
15.
$=14a^2(-x+2y)+7a(-x+2y)$
$=7a(-x+2y)(2a+1)$