
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = 1^2 + 2^2 + 3^2 + ...+ 100^2
A = 1.1 + 2.2 + 3.3 + ... + 100.100
A = 1.(2 - 1) + 2.(3 - 1) + 3.(4 - 1) + ... + 100.(101 - 1)
A = 1.2 - 1 + 2.3 - 2 + 3.4 - 3 + ... + 100.101 - 100
A = (1.2 + 2.3 + 3.4 + ... + 100.101) - (1 + 2 + 3 + ... + 100)
đặt B = 1.2 + 2.3 + 3.4 + ... + 100.101
3B = 1.2.3 + 2.3.3 +3.4.3 + ... + 100.101.3
3B= 1.2.3 + 2.3.(4 - 1) + 3.4.(5 - 2) + ... + 100.101.(102 - 99)
3B = 1.2.3 + 2.3.4 - 1.2.3 + 2.3.4 -3.4.5 + ... +99.100.101 -100.101.102
3B = 99.100.101
B = 99.100.101 : 3
B = 33.100.101
Vậy B = 333300 (1)
Đặt C = 1 + 2 + 3 + ... + 100
C =
Tổng = (Số đầu + số cuối)*số lượng các số trong dãy / 2
Để tính số lượng các số trong dãy chúng ta lấy số cuối - số đầu + 1
Vậy C = (1+100)*100:2 = 5050 (2)
Từ (1) và (2) có:
A = B - C = 333300 - 5050 = 328250

\(a,\sqrt{2}=1,414213562...\)
\(b,\sqrt{60}=2\sqrt{15}=7,745966692...\)
\(c,\sqrt{2008}=2\sqrt{502}=44,810713...\)

Giả sử ta đang cần tìm căn bậc hai của x
Bước 0: Chọn một số mà bạn “nghĩ” là căn bậc hai của x. Gọi nó là g
Bước 1: Tính \(g^2\) . Nếu \(x=g^2\) thì g là số thỏa mãn. Bài toán được giải
Bước 2: Tính \(\frac{1}{2}\left(g+\frac{x}{g}\right)\) Gán nó vào g . Quay lại bước 1


@duc7bthcsct tính thử rùi nhưng sợ sai nên hỏi cho chắc!

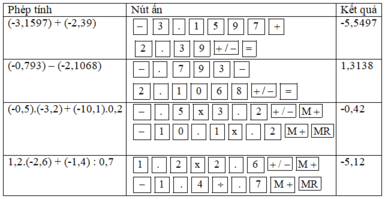
a) (-3,1597)+(-2,39) = -5,5497
b) (-0,793) – (-2,1068) = 1,3138
c) (-0,5).(-3,2)+(-10,1).0,2 = -0,42
d) 1,2.(-2,6) + (-1,4) : 0,7 = -5,12

a) \(\frac{1}{8}.16^n=2^n\)
\(\frac{2^n}{16^n}=\frac{1}{8}\)
\(\left(\frac{2}{16}\right)^n=\frac{1}{8}\)
\(\left(\frac{1}{8}\right)^n=\frac{1}{8}\)
=> n = 1

a=2\(^{12}\).3\(^8\)
=(2\(^3\))\(^4\).(3\(^2\))\(^4\)
=8\(^4\).9\(^4\)
=(8.9)\(^4\)
=72\(^4\)
Nhớ tick đó nha (Tại vì mk là người đầu tiên trả lời mừ
(Tại vì mk là người đầu tiên trả lời mừ )
)