Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Khối 20 mặt đều thuộc loại (3 ;5), nên ta có 3.20 = 5d, suy ra d = 12

Đáp án D
Cách 1. Dựa vào lí thuyết (nhận xét b)
Cách 2. Khối 12 mặt đều thuộc loại (5 ;3) nên ta có 5.12=3d=2c. Suy ra d=20.

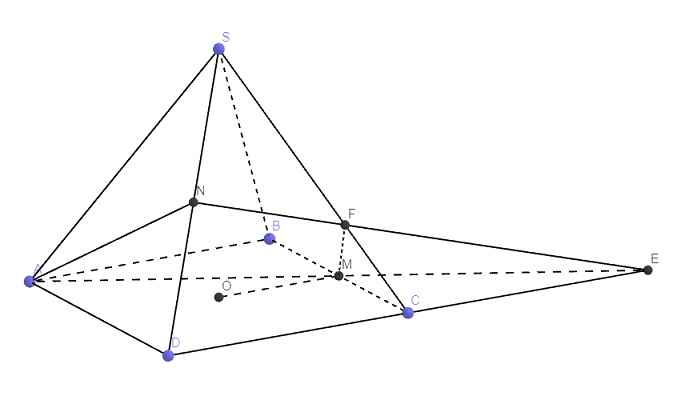
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\Rightarrow\widehat{SMO}=60^0\)
\(\Rightarrow SO=OM.tan60^0=\dfrac{a\sqrt{3}}{2}\)
Trong mp (ABCD), kéo dài AM và CD cắt nhau tại E
Trong mp (SCD), nối NE cắt SC tại F
Theo định lý talet: \(\dfrac{EC}{ED}=\dfrac{MC}{AD}=\dfrac{1}{2}\Rightarrow\left\{{}\begin{matrix}EC=a\\ED=2a\end{matrix}\right.\)
Áp dụng định lý Menelaus cho tam giác SCD:
\(\dfrac{FS}{FC}.\dfrac{CE}{ED}.\dfrac{DN}{NS}=1\Leftrightarrow\dfrac{FS}{FC}.\dfrac{1}{2}.1=1\Rightarrow\dfrac{FS}{FC}=2\)
\(\Rightarrow\dfrac{FC}{SC}=\dfrac{1}{3}\Rightarrow d\left(F;\left(ABCD\right)\right)=\dfrac{1}{3}d\left(S;\left(ABCD\right)\right)=\dfrac{1}{3}SO=\dfrac{a\sqrt{3}}{6}\)
\(ND=\dfrac{1}{2}SD\Rightarrow d\left(N;\left(ABCD\right)\right)=\dfrac{1}{2}d\left(S;\left(ABCD\right)\right)=\dfrac{1}{2}SO=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow V_{NADMFC}=V_{NADE}-V_{FMCE}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{4}.\dfrac{1}{2}a.2a-\dfrac{1}{3}.\dfrac{a\sqrt{3}}{6}.\dfrac{1}{2}.a.\dfrac{a}{2}=\dfrac{5\sqrt{3}}{72}a^2\)
\(\Rightarrow V_1=V_{SABCD}-V_{NADMFC}=....\)


Chọn C
Phương pháp:
Đa giác đều có n cạnh (với n chẵn) thì luôn tồn tại đường chéo là đường kính của đường tròn ngoại tiếp. Từ đó sử dụng kiến thức về tổ hợp để tính toán.

Cách giải:
Số hình vuông tạo thành từ các đỉnh của đa giác đều 20 cạnh là 20: 4 = 5 hình vuông (do hình vuông có 4 cạnh bằng nhau và 4 góc bằng nhau)
Vì đa giác đều có 20 đỉnh nên có 10 cặp đỉnh đối diện hay có 10 đường chéo đi qua tâm đường tròn ngoại tiếp.
Cứ mỗi 2 đường chéo đi qua tâm đường tròn ngoại tiếp tạo thành một hình chữ nhật nên số hình chữ nhật tạo thành là C 10 2 hình trong đó có cả những hình chữ nhật là hình vuông.
Số hình chữ nhật không phải hình vuông tạo thành là C 10 2 - 5 = 40 hình.

Đáp án C
Cách 1. Dựa vào lí thuyết (nhận xét c)
Cách 2. Mỗi mặt của nó là tam giác đều nên số cạnh của nó bằng

Chọn đáp án B
Khối 20 mặt đều có 12 đỉnh.