Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Dựa vào công thức tính công suất hao phí: 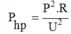
Ta thấy khi công suất truyền tải tăng lên 2 lần thì hao phí truyền tải tăng lên 4 lần

Ta có: \(P_{hp}=\dfrac{P^2\cdot R}{U^2}\)
Mà \(R=\dfrac{l}{S}\cdot\rho\)
Từ hai công thức trên ta suy ra: \(P_{hp}=\dfrac{P^2\cdot R\cdot\rho}{U^2\cdot S}\)
Nhìn vào công thức nếu giảm \(S\) 2 lần và tăng \(U\) 2 lần thì \(P_{hp}\) giảm 2 lần do \(P_{hp}\) tỉ lệ nghịch với \(U^2,S\)

Đáp án D
Hiệu suất truyền tải lúc đầu là 85% nên công suất hao phí lúc đầu là 15% công suất nguồn
Công suất hao phí lúc ban đầu là:
0,15. 5000000 = 750000 (W)
Áp dụng công thức 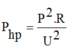
→ Điện trở dây dẫn giảm đi bao nhiêu lần thì công suất hao phí giảm đi bấy nhiêu lần
Công suất hao phí lúc sau là:
750000: (100:60) = 450000 (W)

Công suất hao phí trên đường dây tải điện:
\(P_{hp}=\dfrac{P^2.R}{U^2}=\dfrac{200000^2.20}{100000^2}=80W\)
Để giảm hao phí 2 lần thì:
\(\dfrac{P_{hp1}}{P_{hp2}}=\dfrac{1}{2}\Leftrightarrow\dfrac{R.\dfrac{P^2}{U'^2}}{R.\dfrac{P^2}{U^2}}=\dfrac{U^2}{U'^2}=\dfrac{1}{2}\)
\(\rightarrow U'=\sqrt{2}.U=\sqrt{2}.100000\)
\(=141421,3562\approx141421,4V\)

Ta áp dụng công thức :\(P_{hp}=R.P_2/U_2.\)
Hiệu điện thế giữa hai đầu dây tải điện là :
\(U=P\sqrt{\dfrac{R}{P_{hd}}}=100000.\sqrt{\dfrac{9}{0,25}}=60000V.\)
\(\text{Từ công thức P_{hp}}=R.\dfrac{P_2}{U_2}\\ \Rightarrow U=P\sqrt{\dfrac{R}{P_{hp}}}=100000.\sqrt{\dfrac{9}{0,25}}=60000V\)
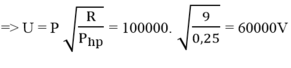
Đáp án D
Khi công suất P tăng lên 2 lần và hiệu điện thế truyền tải U tăng lên 2 lần thì công suất hao phí không thay đổi.