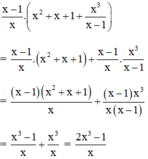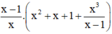Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


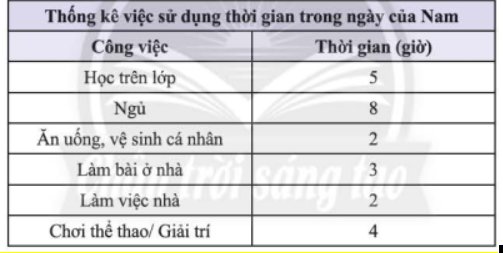
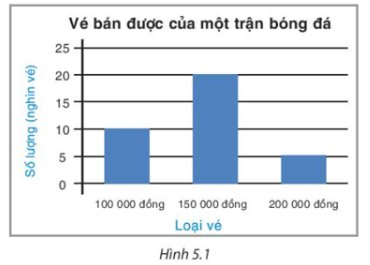
Ta lập bảng thống kê cho dữ liệu được biểu diễn trong biểu đồ trên như sau:
Loại vé | 100 000 đồng | 150 000 đồng | 200 000 đồng |
Số lượng (nghìn vé) | 10 | 20 | 5 |
Để biểu diễn dữ liệu Bảng 5.1, ta nên chọn biểu đồ tranh.
Ta chọn mỗi biểu tượng biểu diễn cho 5 nghìn vé.
Khi đó, số biểu tượng biểu tượng cần biểu diễn số vé 100 000 đồng là:
10 : 5 = 2 (biểu tượng)
Số biểu tượng biểu tượng cần biểu diễn số vé 150 000 đồng là:
20 : 5 = 4 (biểu tượng)
Số biểu tượng biểu tượng cần biểu diễn số vé 200 000 đồng là:
5 : 5 = 1 (biểu tượng)
Ta vẽ biểu đồ tranh như sau:
Loại vé 100 000 đồng | ☺ ☺ |
Loại vé 150 000 đồng | ☺ ☺ ☺ ☺ |
Loại vé 200 000 đồng | ☺ |
(Mỗi ☺ ứng với 5 nghìn vé)

Nên sử dụng biểu đồ cột.
Vì ƯCLN(13,46,183) = 1 nên nếu dùng biểu đồ tranh sẽ phải vẽ rất nhiều biểu tượng (13 + 47 + 183 = 243 (biểu tượng))

Đáp án đúng là: D
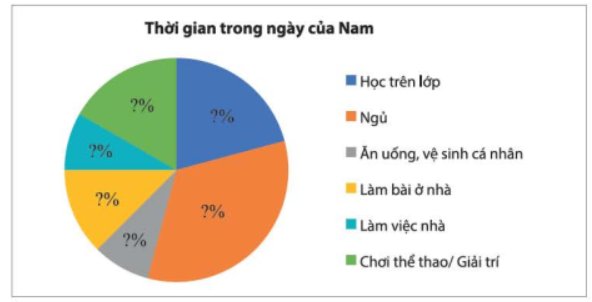
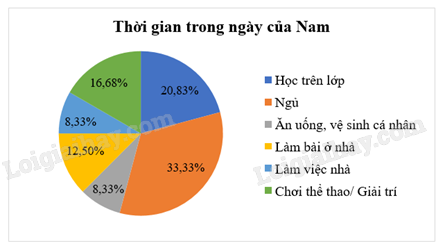
Để biểu diễn tỉ lệ của các phần trong tổng thể ta dùng biểu đồ hình quạt tròn.

Ta có: 1 giây = \(\dfrac{1}{{60}}\) phút
1GB = 1024MB => 4GB = 4.1024 = 4096MB
a) Hàm số f(x) biểu thị dung lượng tiêu tốn (MB) theo thời gian sử dụng internet được x (giây) là: \(f(x) = \dfrac{x}{{60}}\)
b) Hàm số biểu thị dung lượng còn lại sau khi sử dụng được x (giây) là: \(g(x) = 4096 - \dfrac{x}{{60}}\) (MB)
c) Ta có 2 phút = 120 giây
Sau khi sử dụng 2 phút thì số dung lượng còn lại là : \(g(120) = 4096 - \dfrac{{120}}{{60}} = 4094(MB)\)

Đáp án đúng là: C
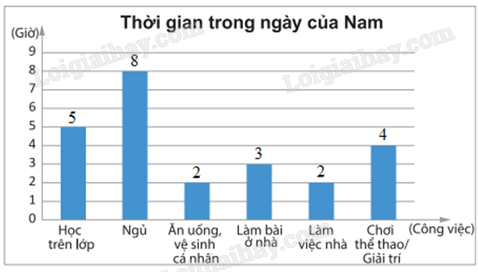
Để biểu diễn sự thay đổi của một đại lượng theo thời gian ta dùng biểu đồ đoạn thẳng.

Ta lập bảng thống kê cho dữ liệu được biểu diễn trong biểu đồ trên như sau:
Loại vé | 100 000 đồng | 150 000 đồng | 200 000 đồng |
Số lượng (nghìn vé) | 10 | 20 | 5 |
Nếu biểu diễn dữ liệu này bằng biểu đồ tranh thì nên chọn mỗi biểu tượng biểu diễn cho 5 nghìn vé vì số liệu 5 nghìn nhỏ nhất trong bảng trên và 10 ⋮ 5; 20 ⋮ 5.

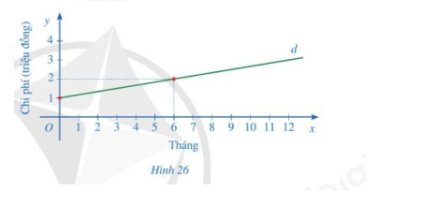
a) Gọi hàm số bậc nhất của đường thẳng d là y = ax + b (a\( \ne \)0)
Từ hình 26, ta thấy đường thẳng d đi qua hai điểm (0; 1) và (6; 2)
Thay tọa độ điểm (0; 1) vào hàm số y = ax + b ta được:
1 = a. 0 + b suy ra b = 1
Hàm số bậc nhất là y = ax + 1 (a\( \ne \)0) (1)
Vì đường thẳng d đi qua điểm (6; 2) nên thay tọa độ điểm (6; 2) vào hàm số (1) ta được là:
2 = a. 6 + 1 suy ra \(a = \dfrac{1}{6}\)
Vậy hàm số của đường thẳng d là \(y = \dfrac{1}{6}x + 1\)
b) Giao điểm của đường thẳng d với trục tung là 1 trong tình huống này có nghĩa là người dùng phải trả khoản phí bạn đầu là 1 triệu đồng
c) Tổng chi phí mà gia đình phải trả khi sử dụng dịch vụ truyền hình với thời gian 12 tháng là ta thay x = 12 vào hàm số \(y = \dfrac{1}{6}x + 1\)
Khi đó: \(y = \dfrac{1}{6}.12 + 1 = 3\)
Tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng là 3 triệu đồng.

Cách 1:Không áp dụng tính phân phối:
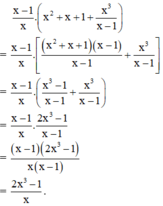
Cách 2: Áp dụng tính chất phân phối: A( B+ C)= AB + AC