
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: y(0) = 0-1= - 1
Và y(-2) = -2 – 1 = - 3
*Xét tính liên tục của hàm số tại x=1
lim x → 1 + y = lim x → 1 + x 2 + 3 x + 1 x − 1 = + ∞ x → 1 + : x − 1 > 0 ; lim x → 1 + ( x − 1 ) = 0 lim x → 1 + ( x 2 + 3 x + 1 ) = 5 > 0
Và lim x → 1 − y = lim x → 1 − ( x − 1 ) = 0
⇒ lim x → 1 + y ≠ lim x → 1 − y
Do đó, hàm số đã cho không liên tục tại x =1
Suy ra, hàm số cũng không có đạo hàm tại x = 1
Chọn D.

+ Trên (-1; +∞), f ( x ) = x 2 - 1 là hàm đa thức nên hàm số liên tục trên khoảng đó.
+ Trên (-∞; -1), f(x) = 3x + 2 là hàm đa thức nên hàm số liên tục trên (-∞; -1).
- Ta xét tính liên tục của hàm số tại điểm x = -1:
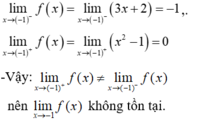
- Do đó f(x) không liên tục tại x= -1 nên A, B, D sai.
Chọn C.

Đáp án B
Phương trình đã cho tương đương với
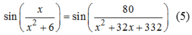
Ta biết rằng hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng 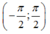
Ta chỉ ra rằng các hàm số ![]() và
và
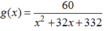 nhận giá trị trong khoảng này.
nhận giá trị trong khoảng này.
Thật vậy 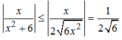
Mặt khác
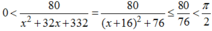
Từ những đánh giá trên, (5) xảy ra khi và chỉ khi
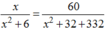
![]()
![]()
Tổng các nghiệm của phương trình đã cho là 2 + 6 + 40 = 48.

Ta có: \({u_n} - {u_{n - 1}} = \left( {3n + 6} \right) - \left[ {3\left( {n - 1} \right) + 6} \right] = 3,\;\forall n \ge 2\)
Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với công sai \(d = 3\).
Chọn đáp án A.
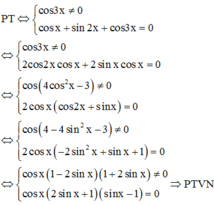
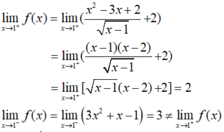
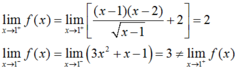
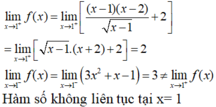
Khẳng định \(3x - 6 = 0 \Leftrightarrow 3x = 6\) đúng