Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do mình không biết vẽ hình như nào nên mình sẽ chỉ giải bài thôi nhé , thoog cảm
Bài 1
Ta có \(\widehat{AOC}+\widehat{BOD}+\widehat{COD}=120^0\)
hay \(30^o+30^o+\widehat{COD}=120^o\)
\(\Rightarrow\widehat{COD}=120^o-30^o-30^o=60^o\)
Mà \(\widehat{AOC}+\widehat{COD}=30^o+60^o=90^o\)
Hay OA vuông góc với OD
Tương tự ta có OB vuông góc với OC
Vậy OA vuông góc với OD ; OB vuông góc với OC

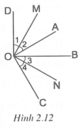
Ta có O C ⊥ O A ⇒ A O C ^ = 90 ° . O D ⊥ O B ⇒ B O D ^ = 90 ° .
Tia OB nằm giữa hai tia OA, OC.
Do đó A O B ^ + B O C ^ = 90 ° . (1)
Tương tự, ta có A O B ^ + A O D ^ = 90 ° . (2)
Từ (1) và (2) ⇒ B O C ^ = A O D ^ (cùng phụ với A O B ^ ).
Tia OM là tia phân giác của góc AOD ⇒ O 1 ^ = O 2 ^ = A O D ^ 2 .
Tia ON là tia phân giác của góc BOC ⇒ O 3 ^ = O 4 ^ = B O C ^ 2 .
Vì A O D ^ = B O C ^ nên O 1 ^ = O 2 ^ = O 3 ^ = O 4 ^ .
Ta có A O B ^ + B O C ^ = 90 ° ⇒ A O B ^ + O 3 ^ + O 4 ^ = 90 ° ⇒ A O B ^ + O 3 ^ + O 2 ^ = 90 ° .
Do đó M O N ^ = 90 ° ⇒ O M ⊥ O N

Đoàn Ngọc Minh Hiếu cóa roảnh
ôg lập lắm nik tek
t vô trag ôg thì ko đăng kí đc TT

Bài 2: ta có: góc AOC+góc AOD=180 độ(vì kề bù) mà góc AOC-AOD= 20 độ => AOC= (180+20):2= 100độ
=> AOD= 100- 20= 80độ
ta có: COB = AOD( vì đối đỉnh)=> COB=80độ
BOD=AOC (vì đối đỉnh)=> BOD=100độ

Bài 1
a
Ta có:
\(\widehat{O_1}=\widehat{O_2}=60^0\left(đ.đ\right)\)
\(\widehat{O_1}+\widehat{O_2}=180^0\Rightarrow\widehat{0_2}=180^0-\widehat{O_1}=180-60^0=120^0\)
\(\widehat{O_2}=\widehat{O_4}=120^0\left(đ.đ\right)\)
b
Ta có:
\(\widehat{x'Oy}=\widehat{y'Ox}\Rightarrow\frac{1}{2}\widehat{x'Oy}=\frac{1}{2}\widehat{y'Ox}\Rightarrow\widehat{yOn}=\widehat{xOm}\)
\(\widehat{x'Oy}+\widehat{yOx}=180^0\)
\(\Rightarrow2\cdot\widehat{yOn}+\widehat{yOx}=180^0\)
\(\Rightarrow\widehat{yOn}+\widehat{yOx}+\widehat{xOm}=180^0\)
\(\Rightarrowđpcm\)
Bài 2
a
Ta có:
\(\widehat{BOD}=\widehat{AOC}=90^0\Rightarrow\widehat{BOC}+\widehat{COD}=\widehat{AOD}+\widehat{COD}\Rightarrow\widehat{BOC}=\widehat{AOD}\)
b
Ta có:
\(\widehat{BOM}=\widehat{BOC}+\widehat{COM}=\widehat{AOD}+\widehat{MOD}=\widehat{MOA}\)
Hiển nhiên OM nằm giữa \(\widehat{AOB}\) nên suy ra đpcm