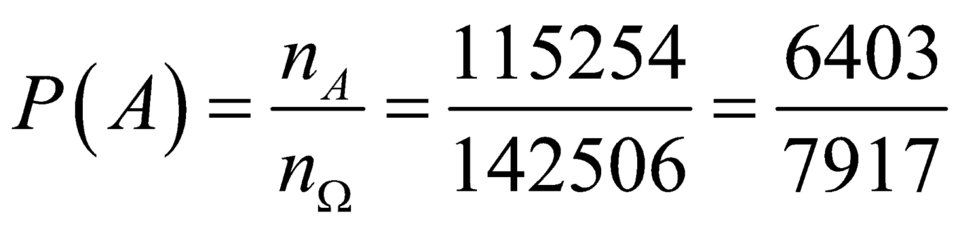Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Không gian mẫu là: Ω = 6 4
TH1: Môn Toán trùng mã đề thi môn Tiếng Anh không trùng có:
Bạn Hùng chọn 1 mã toán có 6 cách và 6 cách chọn mã môn Tiếng Anh khi đó Vương có 1 cách là phải giống Hùng mã Toán và 5 cách chọn mã Tiếng Anh có 6.1.6.5 = 180 cách.
TH2: Môn Tiếng Anh trùng mã đề thi môn Toán không trùng có: 6.1.6.5 = 180 cách.
Vậy P = 180 + 180 6 4 = 5 18

Đáp án D
Một bạn học sinh làm 2 môn sẽ có 36 cách chọn đề, do đó ![]()
Hai bạn Hùng và Vương có chung một mã đề thi thì cùng mã toán hoặc cùng mã tiếng anh do đó ![]()
Vậy xác suất cần tính là 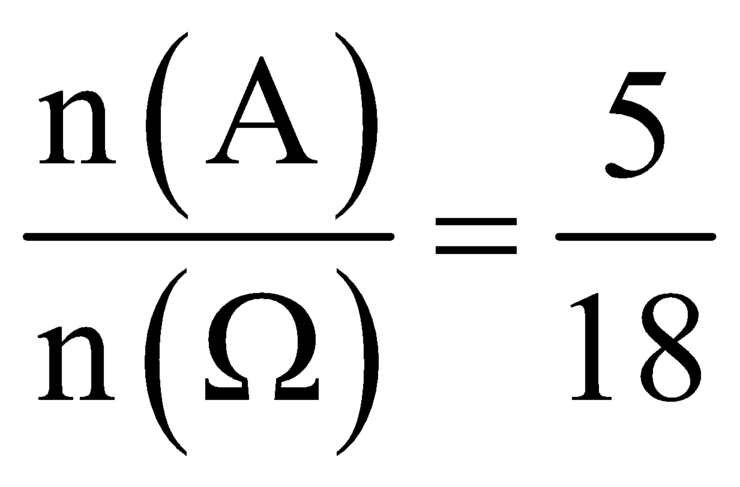

Đáp án A
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố“3 học sinh được chọn luôn có học sinh chọn môn Vật lý và học sinh chọn môn Hóa học”.
Số phần tử của biến cố A là
![]()
Vậy xác suất cần tìm là
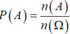
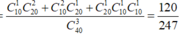

Không gian mẫu : " Chọn 5 học sinh bất kì để đăng kí dự thi " là C530 cách

Chọn B
Số phần tử của không gian mẫu là ![]()
- Gọi A là biến cố “3 học sinh được chọn luôn có học sinh chọn môn Vật lý và học sinh chọn môn Hóa học”
- Số phần tử của biến cố A là
![]()
Vậy xác suất để xảy ra biến cố A là
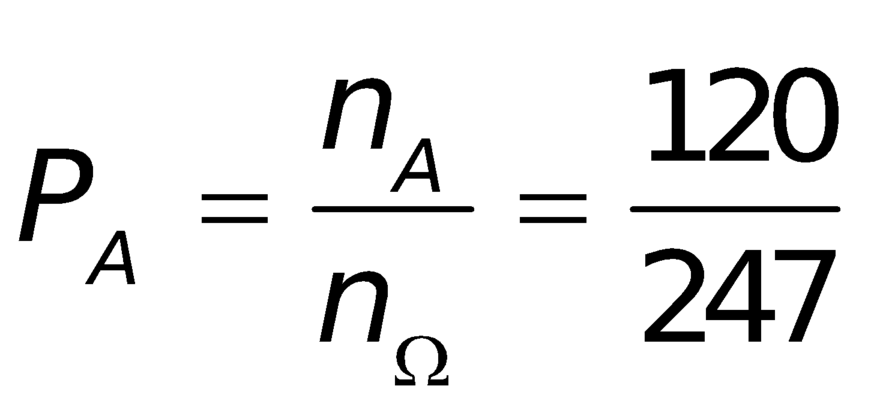 .
.

Đáp án A.
Phương pháp: Tính xác suất để học sinh đúng thêm 3 câu nữa trở lên.
Xác suất mỗi câu trả lời đúng là 0,25 và mỗi câu trả lời sai là 0,75.
Cách giải:
An trả lời chắc chắn đúng 45 câu nên có chắc chắn 9 điểm.
Để điểm thi ≥ 9,5 => An phải trả lời đúng từ 3 câu trở lên nữa.
Xác suất để trả lời đúng 1 câu hỏi là 0,25 và trả lời sai là 0,75
TH1: Đúng 3 câu. P1 = 0,253.0,752
TH2: Đúng 49 câu P2 = 0,254.0,75
TH3: Đúng cả 50 câu P3 = 0,254
Vậy xác suất để An được trên 9,5 điểm là P = P1 + P2 + P3 = 13/1024.