
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\left(\sqrt{5}+1-\sqrt{3}\right)\left(\sqrt{5}-1\right)\)
\(=4-\sqrt{15}+\sqrt{3}\)

\(\hept{\begin{cases}\frac{y}{2}-\frac{\left(x+y\right)}{5}=0,1\\\frac{y}{5}-\frac{\left(x-y\right)}{2}=0.1\end{cases}}\)
\(\hept{\begin{cases}\frac{\left(x+y\right)}{5}=\frac{y-0,2}{2}\\\frac{y}{5}-\frac{\left(x-y\right)}{2}=0,1\end{cases}}\)
\(\hept{\begin{cases}x+y=\frac{5y-1}{2}\\\frac{y}{5}-\frac{\left(x-y\right)}{2}=0,1\end{cases}}\)
\(\hept{\begin{cases}x=\frac{5y-1}{2}-\frac{2y}{2}=\frac{3y-1}{2}\\\frac{y}{5}-\frac{\left(x-y\right)}{2}=0,1\end{cases}}\)
Ta thay x vào biểu thức \(\frac{y}{5}-\frac{\left(x-y\right)}{2}\)ta đc
\(\frac{y}{5}-\frac{\left(\frac{3y-1}{2}-y\right)}{2}=0,1\)
\(\frac{3y-1-2y}{2}=\frac{y}{5}-\frac{0,5}{5}\)
\(\frac{y-1}{2}=\frac{y-0,5}{5}\)
\(5y-5=2y-1\Leftrightarrow5y-5-2y+1=0\Leftrightarrow3y-4=0\Leftrightarrow y=\frac{4}{3}\)
Thay y vào biểu thức \(\frac{3y-1}{2}\)ta đc
\(x=\frac{3.\frac{4}{3}-1}{2}=\frac{3}{2}\)
Vậy \(\left\{x;y\right\}=\left\{\frac{3}{2};\frac{4}{3}\right\}\)

\(\int^{\frac{1}{x}+\frac{1}{y}=\frac{1}{12}}_{\frac{9}{x}+\frac{6}{y}=\frac{3}{4}}\) đặt 1/x=a 1/y=b
hệ pt trở thành \(\int^{a+b=\frac{1}{12}}_{9a+6b=\frac{3}{4}}\)
đến đây bấm máy hoặc giải ra là được

d: góc CEB=góc CAB=90 độ
=>CEAB nội tiếp
góc EAC=góc EBC
góc ECA=góc EBA
mà góc EBC=góc EBA
nên góc EAC=góc ECA
=>EA=EC

This is olm ,not is Scratch ,do you know it ?And no ,i don' t study Scratch !!!

Phương pháp giải bất đẳng thức và cực trị ( dành cho học sinh 8,9) của Nguyễn Văn Dũng-Võ quốc bá cẩn-Trần quốc anh
Nhà xuất bản Đại học quốc gia Hà Nội
quyển màu xanh lá cây bên trên có viền vàng bạn nha! quyển này hay lắm!
Bạn thi HSG cấp tỉnh à?

Thể tích của hình trụ là: \(V=S.h=m^2\pi h\).
Thể tích của hình nón là: \(V=\dfrac{1}{3}S.h=\dfrac{1}{3}m^2\pi h\).
Do đó độ cao trong hình trụ là \(\dfrac{1}{3}h\).
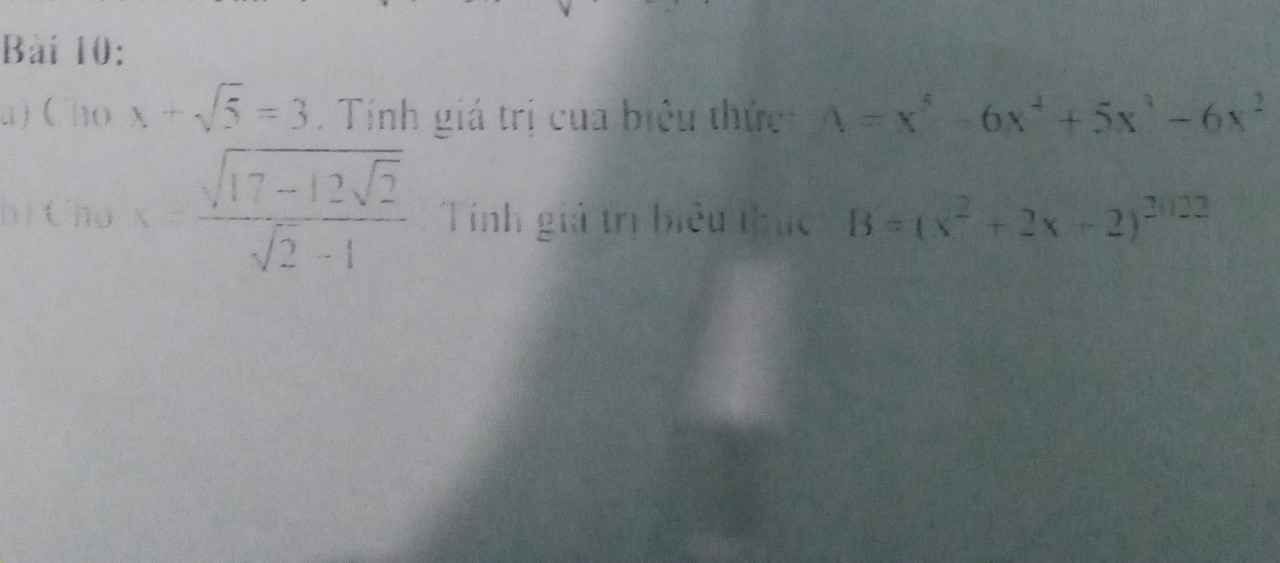
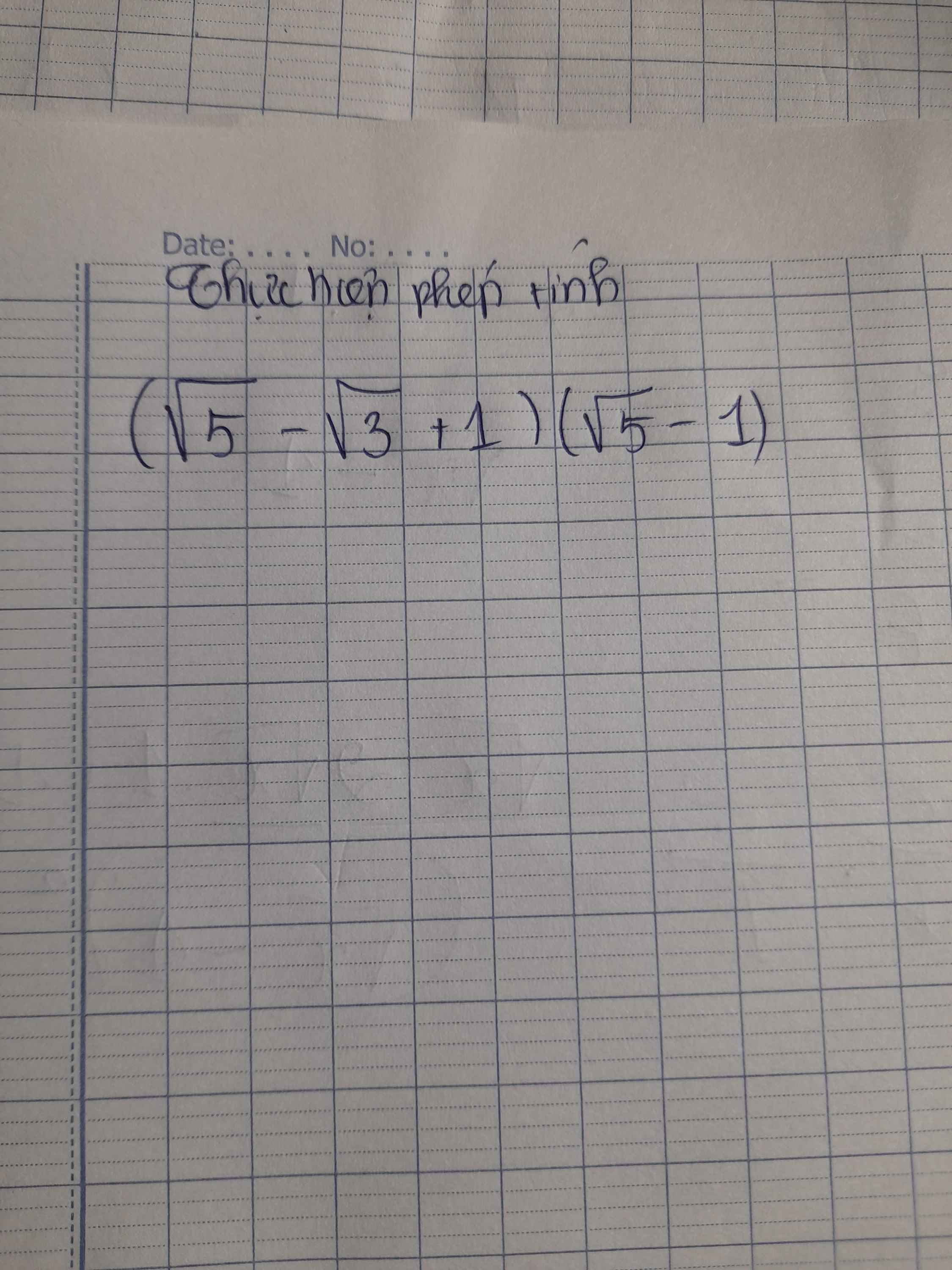

 Ai chỉ em với câu c với khó quá huhu
Ai chỉ em với câu c với khó quá huhu 





b: \(x=\dfrac{\sqrt{17-12\sqrt{2}}}{\sqrt{2}-1}=\dfrac{3-2\sqrt{2}}{\sqrt{2}-1}=\sqrt{2}-1\)
\(B=\left(x^2+2x+2\right)^{2022}\)
\(=\left(3-2\sqrt{2}+2\sqrt{2}-2+2\right)^{2022}\)
\(=3^{2022}\)