Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Another alternative explanation.
Mark the leftmost square crossed of each row as ‘r’, and the topmost crossed square of each column with ‘c’. Thus, each square can be marked either ‘r’ or ‘c’ or ‘both r and c’ or ‘neither r nor c’. We’ll examine each case.
For a square to be marked both ‘r’ and ‘c’, the diagonal must pass through the upper left corner of the square.
For square to be marked ‘r’, diagonal should pass through its upper edge.
For square to be marked ‘c’, diagonal must pass through its left edge.
For square to be marked neither ‘r’ nor ‘c’, diagonal must pass through it’s upper as well as left edge, which is not possible. Therefore, no triangles are unmarked.
Now, no. of squares crossed = no. of squares marked ‘r’ + no. of squares marked ‘c’ - no. of squares marked both ‘r’ and ‘c’
Now, no. of r’s = no. of rows (only 1 leftmost crossed square in each row)
no. of c’s = no. of columns (only 1 topmost crossed square in each column)
all rows and columns are crossed by the diagonal.
Therefore, squares crossed = rows + columns - (no. of squares marked both ‘r’ and ‘c’)
Now, only 1 square is marked both ‘r’ and ‘c’ as 199 and 991 are coprime.
Therefore squares crossed = 199 + 991 - 1 = 1189
Look at this video if you want a clearer visual explanation:

Tham khảo:
Another alternative explanation.
Mark the leftmost square crossed of each row as ‘r’, and the topmost crossed square of each column with ‘c’. Thus, each square can be marked either ‘r’ or ‘c’ or ‘both r and c’ or ‘neither r nor c’. We’ll examine each case.
For a square to be marked both ‘r’ and ‘c’, the diagonal must pass through the upper left corner of the square.
For square to be marked ‘r’, diagonal should pass through its upper edge.
For square to be marked ‘c’, diagonal must pass through its left edge.
For square to be marked neither ‘r’ nor ‘c’, diagonal must pass through it’s upper as well as left edge, which is not possible. Therefore, no triangles are unmarked.
Now, no. of squares crossed = no. of squares marked ‘r’ + no. of squares marked ‘c’ - no. of squares marked both ‘r’ and ‘c’
Now, no. of r’s = no. of rows (only 1 leftmost crossed square in each row)
no. of c’s = no. of columns (only 1 topmost crossed square in each column)
all rows and columns are crossed by the diagonal.
Therefore, squares crossed = rows + columns - (no. of squares marked both ‘r’ and ‘c’)
Now, only 1 square is marked both ‘r’ and ‘c’ as 199 and 991 are coprime.
Therefore squares crossed = 199 + 991 - 1 = 1189

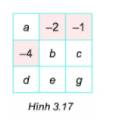
a) Tổng các số trong bảng = Tổng các hàng
Mà tổng các hàng bằng 0 nên tổng các số trong bảng đó bằng 0.
b) Xét hàng số 1 ta có:
a + (-2) + (-1) = 0 => a + (-3) = 0 => a = 3
Xét cột số 1 ta có:
3 + (-4) + d = 0 => (-1) + d = 0 => d = 1.
Xét đường chéo chứa b và d có:
(-1) + b + d = 0 => (-1) + b +1 = 0 => b = 0.
Xét cột số 2 ta có:
(-2) + 0 + e = 0 => e = 2
Xét dòng số 2 có:
-4 + b + c = 0 => -4 + 0 + c = 0 => c =4
Xét dòng số 3 có:
d + e + g = 0 => 1 + 2 + g = 0 => g = -3

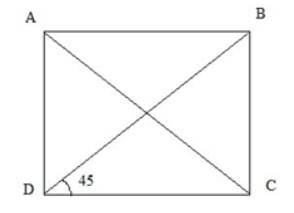
Góc tạo bởi một đường chéo và một cạnh hình vuông bằng 45 độ.

Diện tích phần gạch lát là :
\(4\)x \(4=16\)\(\left(m\right)\)
Số gạch lát sàn là :
\(16:4=6\)( viên)
đs.............