Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

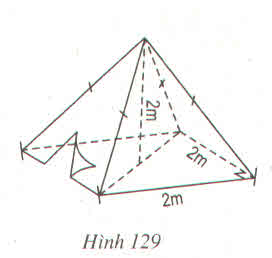
Thể tích cần tính bằng thể tích của hình chóp có chiều cao 2cm
Đáy là hình vuông cạnh dài 2m. Diện tích đáy Sđ = 22 = 4(m2)
Thể tích hình chóp : V = 1313.S.h = 1313.4.2 = 8383
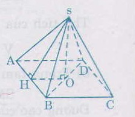
b) Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh) mỗi mặt là một tam giác cân.
Để tính diện tích xung quanh ta cần phải tính được trung đoạn tức là đường cao SH của mỗi mặt
SH2 = SO2 + OH2 = SO2+ (BC2)2(BC2)2 = 22 + 12 = 5
SH = √5 ≈ 2,24m
Nên Sxq = p.d = 1212 2.4.2.24 = 8,96 (m2)
Thể tích cần tính bằng thể tích của hình chóp có chiều cao 2cm
Đáy là hình vuông cạnh dài 2m. Diện tích đáy Sđ = 22 = 4(m2)
Thể tích hình chóp : \(V=\dfrac{1}{3}.S.h=\dfrac{1}{3}.4.2=\dfrac{8}{3}\)

b) Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh) mỗi mặt là một tam giác cân.
Để tính diện tích xung quanh ta cần phải tính được trung đoạn tức là đường cao SH của mỗi mặt
\(SH^2=SO^2+OH^2=SO^2+\left(\dfrac{BC}{2}\right)^2=2^2+1^2=5\)
\(SH=\sqrt{5}\approx2,24m\)
Nên Sxq = p.d = \(\dfrac{1}{2}\) 2.4.2.24 = 8,96 (m2)

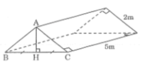
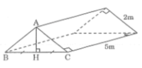
a) Lều là lăng trụ đứng tam giác.
Diện tích đáy (tam giác):
S=12.3,2.1,2=1,92(m2)S=12.3,2.1,2=1,92(m2)
Thể tích khoảng không bên trong lều là:
V = Sh = 1,92. 5 = 9,6 (m3)
b) Số vải bạt cần có để dựng lều chính là diện tích toàn phần của lăng trụ trừ đi diện tích mặt bên có kích thước là 5m và 3,2m.
Diện tích xung quanh lăng trụ là:
Sxq = 2ph = (2 + 2+ 3,2) .5 = 36 (m2)
Diện tích toàn phần:
Stp = Sxq + 2Sđ = 36 + 2.1,92 = 39,84 (m2)
Diện tích mặt bên kích thước 5m và 3,2m là:
S = 5.3,2 = 16 (m2)
Vậy số vải bạt cần có để dựng lều là:
39,84 – 16 = 23,84 (m2)
Chú ý:Có thể tính bằng cách khác là tổng diện tích hai mặt bên và hai đáy.

Lều là lăng trụ đứng đáy tam giác vuông cân, cạnh 2m, chiều cao lăng trụ 5m.
Diện tích đáy là: Sđáy =12 .2.2=2 ( m 2 )
Thể tích lều là: V= S.h = 2.5 = 10 ( m 3 )

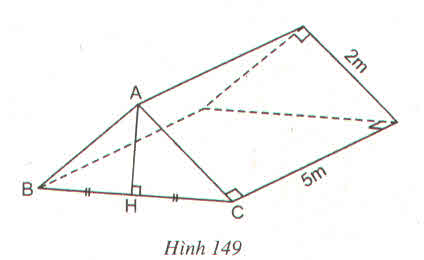
a)Ta có E là trung điểm của CM (gt)
F là trung điểm của CB (gt)
\(\Rightarrow\) EF là đường trung bình của (định nghĩa đường trung bình của tam giác)
\(\Rightarrow\) EF//MB (tính chất đường trung bình của tam giác)
hay EF//AB
lại có K là trung điểm của AD (gt)
F là trung điểm của CB (gt)
\(\Rightarrow\) KF là đường trung bình của (...)
\(\Rightarrow\) KF//AM (t/c ...)
hay KF//AB
nên EF//KF (vì cùng // với AB)
\(\Rightarrow\) tứ giác EFFIK là hình thang (Định nghĩa hình thang)
Gọi N là trung điểm của AM, nối KM
Ta có N là trung điểm của AM (cách dựng)
K là trung điểm của AD (gt)
\(\Rightarrow\) NK là đường trung bình của
nên NK//DM (t/c....)
mà EN là đường trung bình của (E,I là trung điểm của MC,AM)
\(\Rightarrow\) EI//AC (t/c...)
lại có và
là những tam giác đều (gt)
\(\Rightarrow\)
\(\Rightarrow\) AC//DM
tức là NK//EN (cùng //AC//DM)
do đó 3 điểm E,K,N thẳng hàng (theo tiên đề Ơ-clit)
(2góc đồng vị của AC//EN)
(2 góc đồng vị của KF//AM)
nên
C/m tương tự, lấy P là trung điểm của BM ta cũng được
Hình thang EFIK có
Vậy EFIK là hình thang cân (dấu hiệu nhận biết)
b) Ta có EFIK là hình thang cân (kq câu a)
\Rightarrow EI=KF (tính chất 2 đường chéo trong hình thang cân)
E là trung điểm của CM, I là trung điểm của DM (gt)
\(\Rightarrow\) EI là đường trung bình của tam giác CMD
\(\Rightarrow\) EI=
Vậy KF=

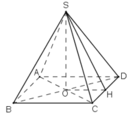
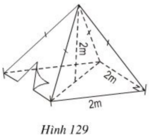
a) Lều là hình chóp đều có đáy là hình vuông cạnh bằng 2m, chiều cao bằng 2m.
Thể tích không khí trong lều bằng thể tích lều và bằng:
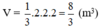
b) Số vải bạt cần thiết đề dựng lều chính là diện tích xung quanh của lều.
Dựng trung đoạn SH.
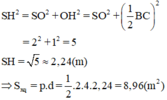

a) Trong tam giác ADC, ta có:
E là trung điểm của AD (gt)
I là trung điểm của AC (gt)
Nên EI là đường trung bình của ∆ ABC
⇒ EI // CD (tính chất đường trung bình của tam giác)
Trong tam giác ABC ta có:
I là trung điểm của AC
F là trung điểm của BC
Nên IF là đường trung bình của ∆ ABC
⇒ IF // AB (tính chất đường trung bình của tam giác)
b) Câu b đou

a:
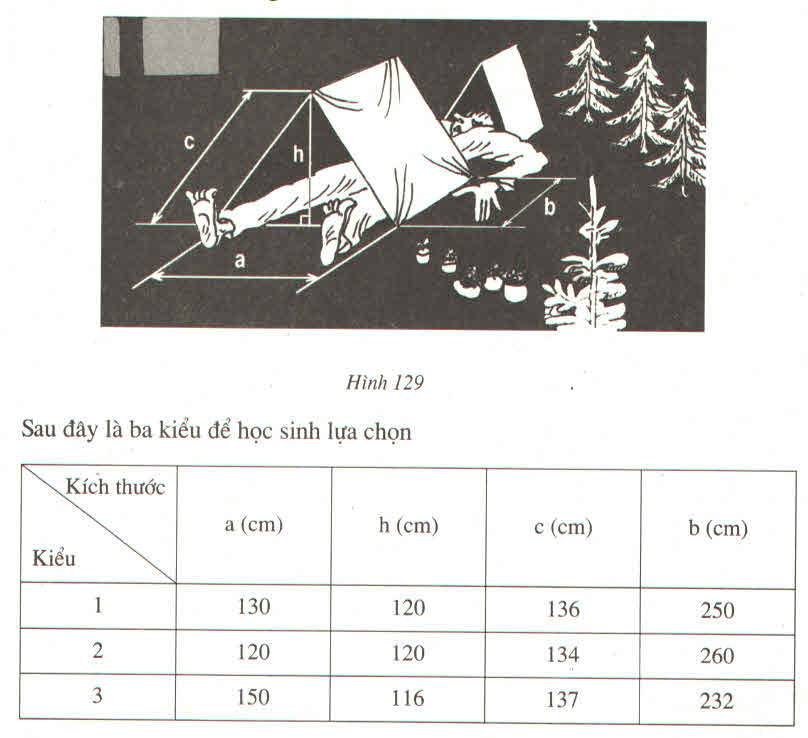
-Kiểu 1: \(S=\dfrac{1}{2}\cdot130\cdot120=7800\left(cm^2\right)\)
\(V=7800\cdot250=1950000\left(cm^3\right)\)
-Kiểu 2: \(S=\dfrac{1}{2}\cdot120\cdot120=7200\left(cm^2\right)\)
\(V=7200\cdot260=1872000\left(cm^3\right)\)
-Kiểu 3: \(S=\dfrac{1}{2}\cdot150\cdot116=8700\left(cm^2\right)\)
\(V=8700\cdot232=2018400\left(cm^3\right)\)
b:
-Kiểu 1:
Diện tích hai mặt bên là:
\(2\cdot136\cdot250=68000\left(cm^2\right)\)
Phần diện tích lều nhận được ánh sáng là:
7800+68000=75800(cm2)
-Kiểu 2:
DIện tích hai mặt bên là:
\(2\cdot134\cdot260=69680\left(cm^2\right)\)
Phần diện tích lều nhận được ánh sáng là;
\(7200+69680=76880\left(cm^2\right)\)
-Kiểu 3:
Diện tích hai mặt bên là:
\(2\cdot137\cdot232=63568\left(cm^2\right)\)
Phần diện tích lều nhận được ánh sáng là:
\(63568+8700=72268\left(cm^2\right)\)
c: Chọn kiều lều 3 vì thể tích lớn nhất



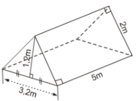


Số vải cần để làm lều là hai mặt bên và hai đầu hồi (hai đáy của lăng trụ đứng)
Diện tích hai mặt bên là : (2.5).2=20 ( m 2 )
Diện tích vải cần dùng là:20+2.2=24 ( m 2 )