
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Đo góc, ta được góc ở đỉnh H của hình thang cân EFGH bằng góc G.
- Các cạnh bên của hình thang cân là EH và FG nên EH = FG (tính chất hình thang cân).
Các đường chéo là EG và FH nên EG = FH (tính chất hình thang cân).

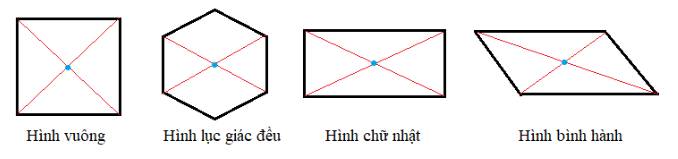
- Tâm đối xứng của hình vuông là giao điểm của hai đường chéo.
- Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
- Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.
- Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
Các hình không có tâm đối xứng: Tam giác đều, hình thang cân.

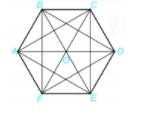
Các hình thang cân: ABCD, BCDE, CDEF, DEFA, EFAB, FABC.
Các hình chữ nhật: ABDE, BCEF, CDFA.

Một số hình ảnh hình thang cân trong thực tế: họa tiết trang trí, cái thang, mặt túi xách, mặt cắt của tòa tháp, ...


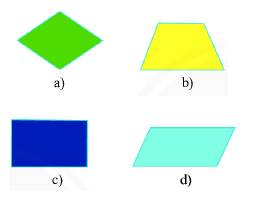
Hình a là hình thoi.
Hình b là hình thang cân.
Hình c là hình chữ nhật.
Hình d là hình bình hành.

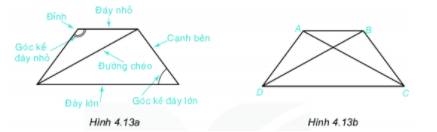
1) Đỉnh: A, B, C, D
Đáy lớn: DC
Đáy nhỏ: AB
Đường chéo: AC, BD
Cạnh bên AD, BC
2) Dùng thước thẳng hoặc compa, ta đo được: AD = BC; AC = BD
Vậy: Hai cạnh bên hình thang cân bằng nhau
Hai đường chéo hình thang cân bằng nhau.
3) Khi đặt eke vuông góc với AB ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
Vậy hai đáy của hình thang cân song song với nhau.
4) Hai góc kề một đáy của hình thang bằng nhau.

Vì tứ giác ABCD là hình thang cân (gt).
=> AD = BC (Tính chất hình thang cân).
Mà BC = 2 (cm).
=> AD = 2 (cm).
Chu vi hình thang ABCD là:
AB + CD + BC + AD = 3 + 5 + 2 + 2 = 12 (cm).
p hình thang cân là :
3 + 5 + 2 + 2 = 12 cm
Đ/S : 12 cm


Hình thang cân trong các hình thang là : HKIJ (vì có HJ = IK)