Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Độ dài đg chéo là \(\sqrt{12^2+9^2}=15\left(cm\right)\left(pytago\right)\)



Đường chéo của hình chia hình chữ nhật thành 2 hình tam giác vuông bằng nhau, có cạnh huyền là 13cm, một trong 2 cạnh kia là 5cm. Gọi cạnh còn lại của hình tam
giác (đây là 1 cạnh của hình chữ nhật,khác cạnh 5cm) là a, ta có:
52+a2=132
=>25+a2=169
=>a2=169-25=144
Vì cạnh hình tam giác là 1 số dương => a=12
Cạnh 5cm là 1 cạnh của hình chữ nhật, mà ta có a=12cm cũng là 1 cạnh của hình chữ nhật
Vậy diện tích hình chữ nhật là:
12x5=60(cm2)
Theo Pi-ta-go,ta có:
\(\sqrt{13^2-5^2}=12\)
Diện tích hình chữ nhật là:
12 • 5 = 60

Đây nhé
ta có a là chiều dài, b là chiều rông, c là chiều cao
theo đề bài ta có: a - b = 3 cm
a + b = 30/2 = 15 cm
a = (15+3) : 2 = 9 cm
b = (15-3) : 2 = 6 cm
c2 = a2 + b2 ( D.lý Pi Ta Go) ==> c2 = 92 + 62 = 81 + 36 = 117
==> c = \(\sqrt{117}\)

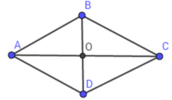
Giả sử hình thoi ABCD có đường chéo AC vuông góc BD tại O, BD = 10 cm; AC = 24 cm.
Suy ra BO = 1 2 BD = 1 2 .12 = 6 (cm);
AO = 1 2 AC = 1 2 .24 = 12 (cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AB = A O 2 + B O 2 = 5 2 + 12 2 = 13 (cm)
Đáp án cần chọn là: C
Lời giải:
Theo định lý Pitago, độ dài cạnh kề với cạnh đã cho của HCN là:
$\sqrt{5^2-3^2}=4$