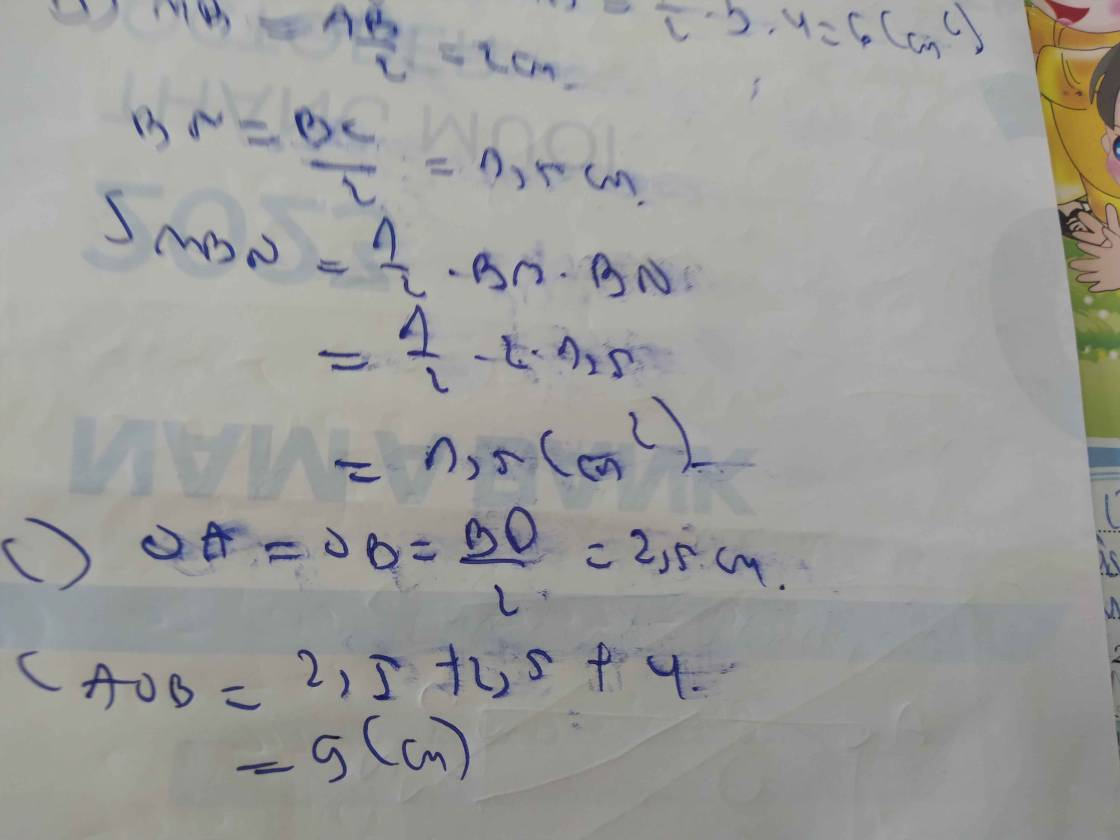TT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 2 2023
2: ΔADE vuông tại D
nên AD<AE
3: h(A;DC)=AD
6: h(C;AD)=CD
7: góc AED<90 độ
=>góc AEF>90 độ
=>AE<AF
25 tháng 6 2021
Bài 1 :
Vì ABCD là hình vuông \(\Rightarrow\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=90^0\)
\(\Rightarrow AB=BC=CD=AD=4\)cm
Áp dụng định lí pytago tam giác ADC vuông tại D ta có :
\(AC^2=AD^2+CD^2=16+16=32\Rightarrow AC=4\sqrt{2}\)cm
Vì ABCD là hình vuông nên 2 đường chéo bằng nhau AC = BD = 4\(\sqrt{2}\)cm
25 tháng 6 2021
Bài 2 :
Vì ABCD là hình chữ nhật nên \(AB=CD;AD=BC\)
Áp dụng định lí Pytago tam giác ACD vuông tại D ta có :
\(AC^2=AD^2+DC^2=27+9=36\Rightarrow AC=6\)cm
13 tháng 5 2022
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
góc BAD chung
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
b: \(BD=\sqrt{10^2-6^2}=8\left(cm\right)\)
d: Xét ΔHBC có \(\widehat{HBC}=\widehat{HCB}\)
nên ΔHBC cân tại H
=>HB=HC
hay H nằm trên đường trung trực của BC(1)
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC(2)
Từ (1) và (2) suy ra A,H,M thẳng hàng
4 tháng 3 2017
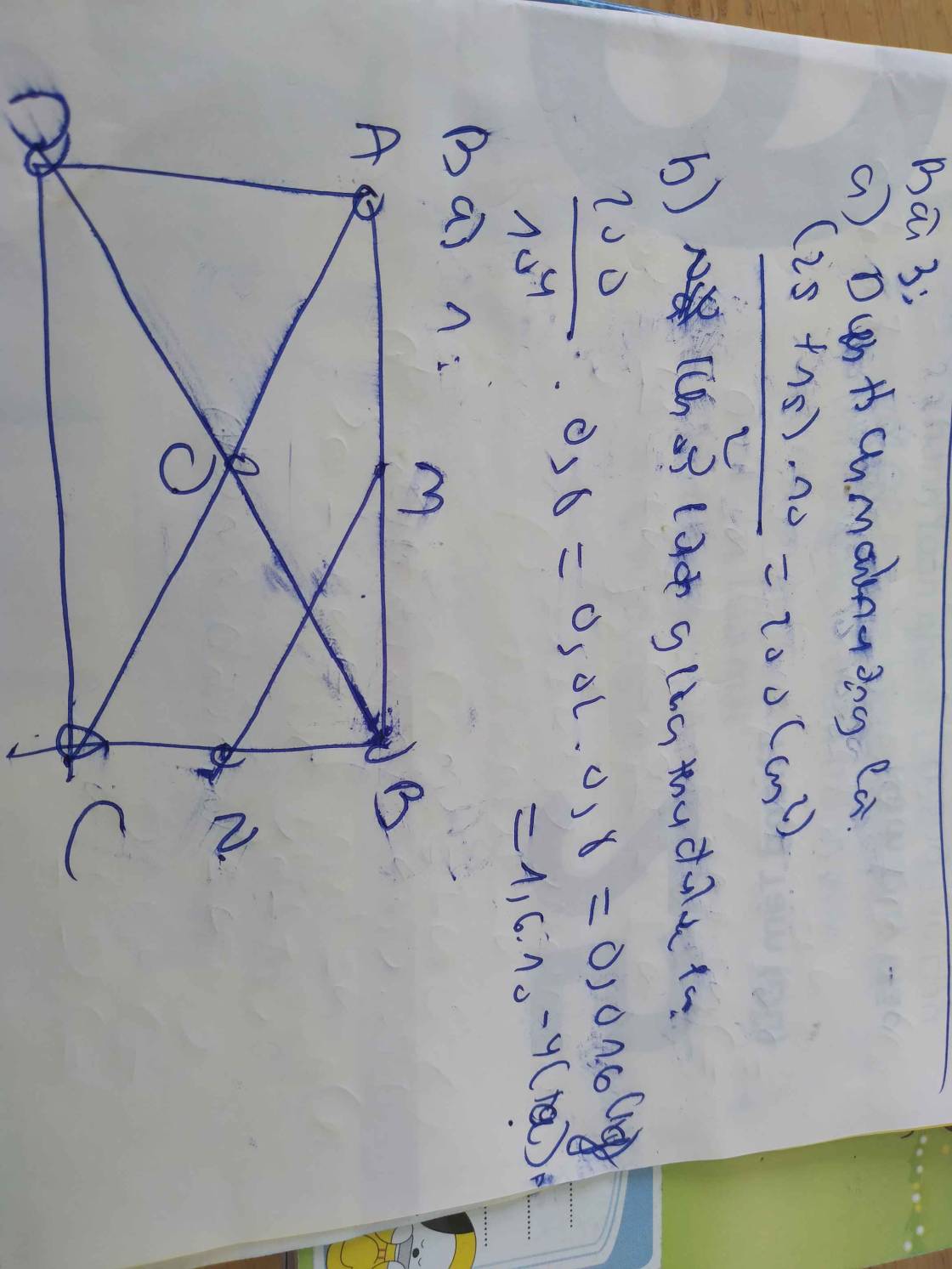
Vì là hình chữ nhật nên hai đường chéo sẽ bằng nhau
Do đó: \(AO=\frac{AC}{2}\)
Mặt khác: ABCD là hình chữ nhật \(\Rightarrow AB=AD=BC=DC=10cm\)
Trong tam giác ADC (\(\widehat{A}=90\)), có:
\(AC^2=AD^2+DC^2\)(định lý Py-ta-go)
\(\Leftrightarrow AC^2=10^2+10^2=200\Rightarrow AC=\sqrt{200}\)
Mà \(AO=\frac{AC}{2}\)(cmt) hay \(AO=\frac{\sqrt{200}}{2}\approx7,07\left(cm\right)\)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
a)
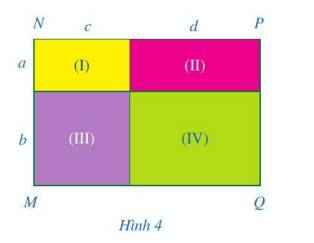
Diện tích của hình chữ nhật (I) là: \(a.c\).
Diện tích của hình chữ nhật (II) là: \(a.d\).
Diện tích của hình chữ nhật (III) là: \(b.c\).
Diện tích của hình chữ nhật (IV) là: \(b.d\).
b) Diện tích hình chữ nhật MNPQ là: \(ac + ad + bc + bd\).
c) Ta có:
\((a + b)(c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd\).
Vậy \((a + b)(c + d)\) = \(ac + ad + bc + bd\).
28 tháng 12 2023
ta có:
AB² + AC² = BC²
15² + 20² = 25²
225 + 400 = 625
625 = 25²
=> BC = 25 cm
Từ đó, ta có:
d = √(AB² + AC² - BC²) = √(15² + 20² - 25²) = √(225 + 400 - 625) = √(165) = 12,8 cm
Vậy, khoảng cách từ A đến BC là 12,8 cm.
28 tháng 12 2023
Cho tam giác ABC,M,N lần lượt là trung điểm AB,AC.Trên tia đối của tia NM xác định điểm P sao cho NP=MN.Chứng minh:
a) CP// AB. b)MB=CP. c) BC=2MN