Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(BO=CO=AO=\dfrac{6\sqrt{3}}{3}=2\sqrt{3}\left(cm\right)\)
\(SB=\sqrt{SO^2+OB^2}=\sqrt{24+12}=6\left(cm\right)\)

Đáy ABCD là hình vuông nên △ OAB vuông cân tại O.
Áp dụng định lí pi-ta-go ta tính được OA bằng 32
Ta có: SO ⊥ OA nên tam giác AOA cân tại O.
Áp dụng Pi-ta-go vào tam giác vuông SOA ta tỉnh được SO bằng 32
Vậy chọn đáp án C.

a:ΔSBC cân tại S có SM là trung tuyến
nên SM vuông góc BC
BC=6cm
=>BM=CM=3cm
SM=căn 5^2-3^2=4cm
Sxq=5*3/2*4=5*3*2=30cm2
Stp=30+5^2*căn 3/2=(60+25căn 3)/2cm2
b: BC vuông góc SM
BC vuông góc AM
=>BC vuông góc (SAM)

Chọn đáp án A
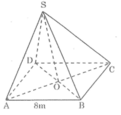
Gọi O là giao điểm của AC và BD.
Áp dụng định lí Pytago vào tam giác vuông ABC có:
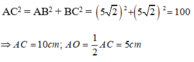
Áp dụng định lí Pytago vào tam giác vuông SAO có:
S O 2 = S A 2 - A O 2 = 13 2 - 5 2 = 144 nên SO = 12cm