

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A

ABCD là hình thanh cân có AB = BC = CD = a; AD = 2a nên M là tâm của đáy ABCD.
SA = AD = 2a; SA ⊥ (ABCD) => tam giác SAD vuông cân tại A nên tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm N của SD
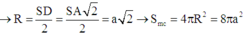

Đáp án A
Ta có SC là đường kính của mặt cầu ngoại tiếp hình chóp S.ABCD vì các góc ở đỉnh A, B, D đều nhìn SC dưới góc 90 độ S B C ^ = S D C ^ = S A C ^ = 90 0 . Do đó bán kính của mặt cầu là R = 1 2 SC.
Tam giác ADC vuông tại D có
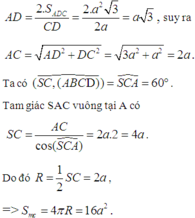

Chọn đáp án D
Gọi O là tâm của hình chữ nhật ABCD và I là trung điểm của SC. Khi đó OI ⊥ (ABCD)
⇒ IA = IB = IC = ID với ∆ S A C vuông tại A, IA = IS = IC. Do đó I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD suy ra IA = a 2 ⇒ SC = 2a 2 . Mặt khác AC là hình chiếu của SC trên mặt phẳng (ABCD).
![]()
Suy ra ∆ S A C vuông cân
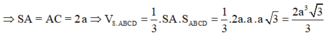

Đáp án A.
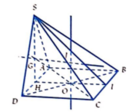
Trong mặt phẳng (ABCD) gọi: ![]() H là trung điểm AD.
H là trung điểm AD.
Gọi I,J lần lượt là trung điểm của BC và G là trọng tâm ∆ SAD
Đường thẳng d qua O và vuông góc với (ABCD) gọi là trục của đường tròn ngoại tiếp đáy (ABCd).
∆ qua G và vuông góc với (SAD) là trục của đường tròn ngoại tiếp (SAD).
Trong mặt phẳng (SHI), gọi I = ∆ ∩ d
=> J cách đều các đỉnh của hình chóp
=> J là tâm mặt cầu ngoại tiếp S.ABCD có bán kính
R = JD = ![]()
Có ![]()
