Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp
Hình chóp có cạnh bên vuông góc với đáy, sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp

Hình chóp có cạnh bên vuông góc với đáy, sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp
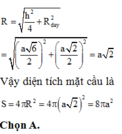

Đáp án A.
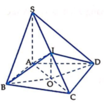
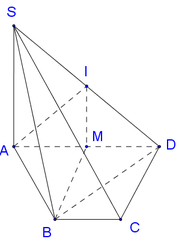
1. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD
Ta có
C B ⊥ A B , C B ⊥ S A , A B ∩ S A = A ⇒ C B ⊥ S A B ⇒ C B ⊥ S B ⇒ Δ S B C
vuông tại B.
Lại có
C D ⊥ A D , C D ⊥ S A , A D ∩ S A = A ⇒ C D ⊥ S A D ⇒ C D ⊥ S D
⇒ Δ S D C vuông tại D.
Mặt khác S A ⊥ A B C D ⇒ S A ⊥ A C ⇒ Δ S A C vuông tại A.
Gọi I là trung điểm của SC. Các tam giác: Δ S A C , Δ S B C , Δ S D C lần lượt vuông tại các đỉnh A, B và D nên I S = I A = I B = I C = I D = 1 2 S C . Vậy mặt cầu ngoại tiếp hình chóp S.ABCD có tâm I, bán kính R = 1 2 S C
2. Tính diện tích mặt cầu
Ta có S C , A B C D ^ = S C , A C ^ = S C A ^ = 60 °
Do Δ A D C vuông tại A nên S ?A C = 1 2 A D . C D ⇔ A D = 2 S Δ A D C C D = a 2 3 a = a 3
⇒ A C = A D 2 + C D 2 = a 3 2 + a 2 = 2 a
Mà A C = S C . cos S C A ^ ⇒ S C = 2 a cos 60 ° = 4 a
Vậy bán kính của mặt cầu ngoại tiếp hình chóp S.ABCD là R = S C 2 = 4 a 2 = 2 a và diện tích mặt cầu là S = 4 π R 2 = 4 π . 2 a 2 = 16 π a 2 (đvdt).

Đáp án A
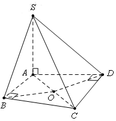
Tam giác ADC vuông tại D ⇒ S Δ A D C = 1 2 . A D . C D = a 2 3 2
⇒ C D = a 3 ⇒ A C = A D 2 + C D 2 = a 2 + a 3 2 = 2 a .
Vì tứ giác ABCD có A B C ⏜ = A D C ⏜ = 90 ∘ ⇒ A B C D là tứ giác nội tiếp đường tròn tâm O với O là trung điểm của AC ⇒ R A B C D = A C 2 = a .
Và S A ⊥ A B C D ⇒ S C ; A B C D ⏜ = S C ; A C ⏜ = S C A ⏜ = 60 ∘
Tam giác SAC vuông tại A ⇒ tan S C A ⏜ = S A A C ⇒ S A = 2 a 3 .
Suy ra bán kính mặt cầu cần tính là:
R = R 2 A B C D + S A 2 4 = 2 a ⇒ S m c = 16 π a 2 .

![]()
![]()
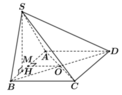
Gọi M là trung điểm AB, do tam giác SAB vuông tại S nên MS = MA = MB
Gọi H là hình chiếu của S trên AB. Từ giả thiết suy ra ![]()
Ta có ![]() nên là trục của tam giác SAB, suy ra OA = OB = OS (2)
nên là trục của tam giác SAB, suy ra OA = OB = OS (2)
Từ (1) và (2) ta có OS = OA = OB = OC = OD.
Vậy O là tâm mặt cầu ngoại tiếp khối chóp S.ABCD bán kính 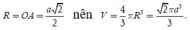
Chọn B.

Đáp án A
Ta có SC là đường kính của mặt cầu ngoại tiếp hình chóp S.ABCD vì các góc ở đỉnh A, B, D đều nhìn SC dưới góc 90 độ


Vì ABCD là hình vuông nên OA = OB = OC (1)
Dễ dàng chứng minh được A H ⊥ H C nên tam giác AHC vuông tại H và có O là trung điểm cạnh huyền AC nên suy ra OH = OC
Từ (1) và (2) suy ra ![]()


Đáp án D
Ta có R = S A 2 4 + R d 2 = a 2 + a 2 2 2 = a 3 2 ⇒ S = 4 π R 2 = 6 π a 2