Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường thẳng đi qua hai điểm (-1 ; 0 ) và (0 ; -2) có phương trình chính tắc là »
x - 1 + y - 2 = 1 ⇔ 2 x + y + 2 = 0
Điểm O(0; 0) thuộc miền bị gạch và 2.0 + 0 + 2 >0 .
Do đó, nửa mặt phẳng không bị gạch biểu diễn miền nghiệm của bất phương trình 2 x + y + 2 ≤ 0
(kể cả bờ là đường thẳng).

Đường thẳng đi qua hai điểm (-1 ; 0 ) và (0 ; -2) có phương trình chính tắc là »
x - 1 + y - 2 = 1 ⇔ 2 x + y + 2 = 0
Điểm O(0; 0) thuộc miền bị gạch và 2.0 + 0 + 2 >0 .
Do đó, nửa mặt phẳng không bị gạch biểu diễn miền nghiệm của bất phương trình 2 x + y + 2 ≤ 0
(kể cả bờ là đường thẳng 2x+y+2=0).
Chọn C

Đường thẳng đi qua hai điểm (1;0) và (0;2) có phương trình là : x 1 + y 2 = 1 ⇔ 2 x + y - 2 = 0
Điểm O(0; 0) thuộc miền bị gạch và 2.0+ 0 – 2 < 0 nên nửa mặt phẳng không bị gạch sọc biểu diễn miền nghiệm của bất phương trình : 2x + y – 2 > 0
Đáp án là D.

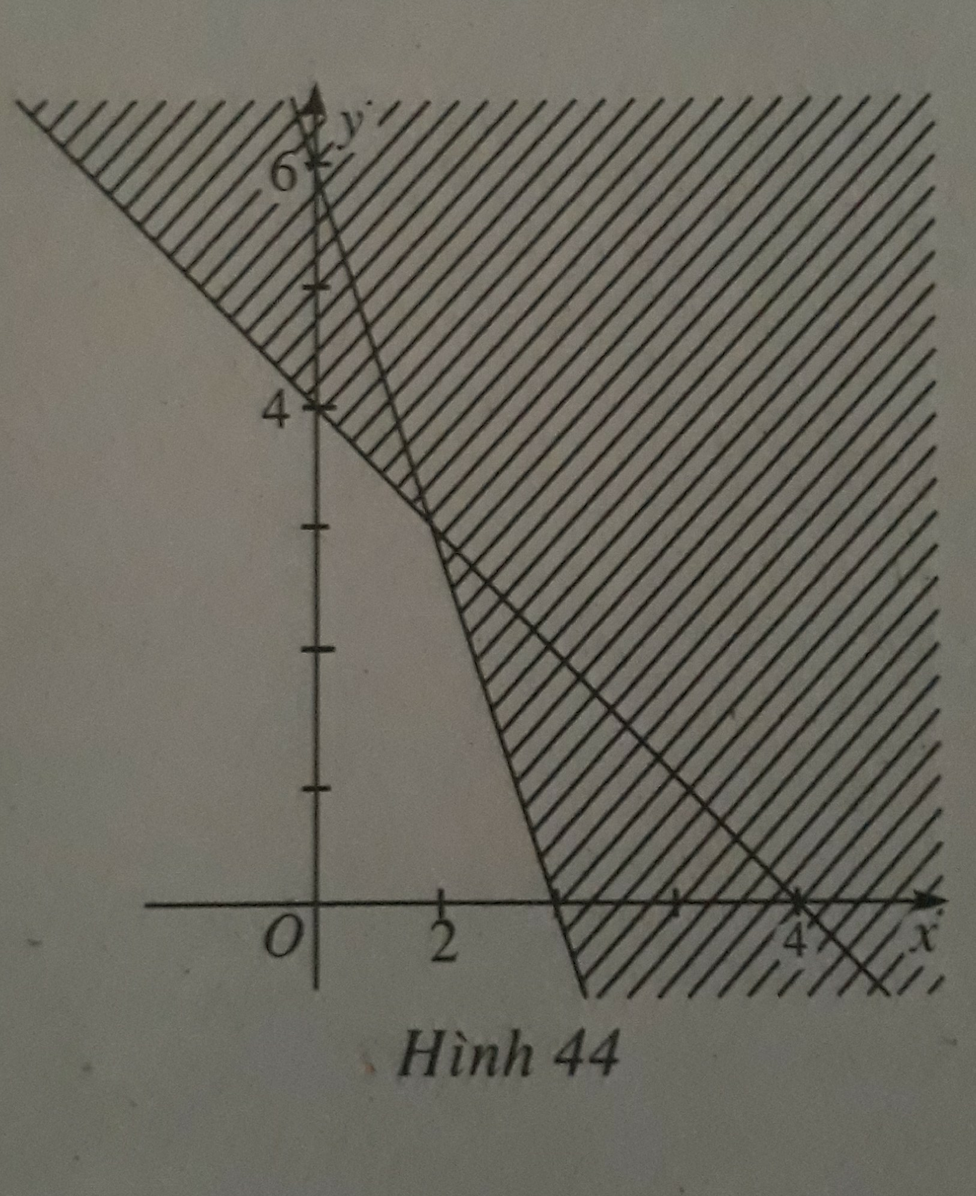
Miền góc không bị gạch được giới hạn bởi hai đường thẳng:
Đường thẳng thứ nhất đi qua hai điểm (6;0) và (0;2) nên có phương trình:
x 6 + y 2 = 1 ⇔ x + 3 y - 6 = 0
Với bờ là đường thẳng x+3y-6=0 theo hình thì gạch bỏ đi phần không chứa O
Do đó nửa mặt phẳng không gạch (chứa O) với bờ là x+3y-6=0 biểu diễn nghiệm của bất phương trình x+3y-6=<0.
Đường thẳng thứ hai đi qua hai điểm (-2;0) và (0;-4) nên có phương trình:
x - 2 + y - 4 = 1 ⇔ 2 x + y + 4 = 0
Với bờ là đường thẳng 2x+y+4=0 theo hình thì gạch bỏ đi phần chứa O
Do đó nửa mặt phẳng không gạch (không chứa O) với bờ là 2x+y+4=0 biểu diễn nghệm của bất phương trình 2x+y+4<0.
Kết hợp 2 miền ta được miền góc không bị gạch là nghiệm của hệ
x + 3 y - 6 < 0 2 x + y + 4 < 0
Chọn đáp án D.

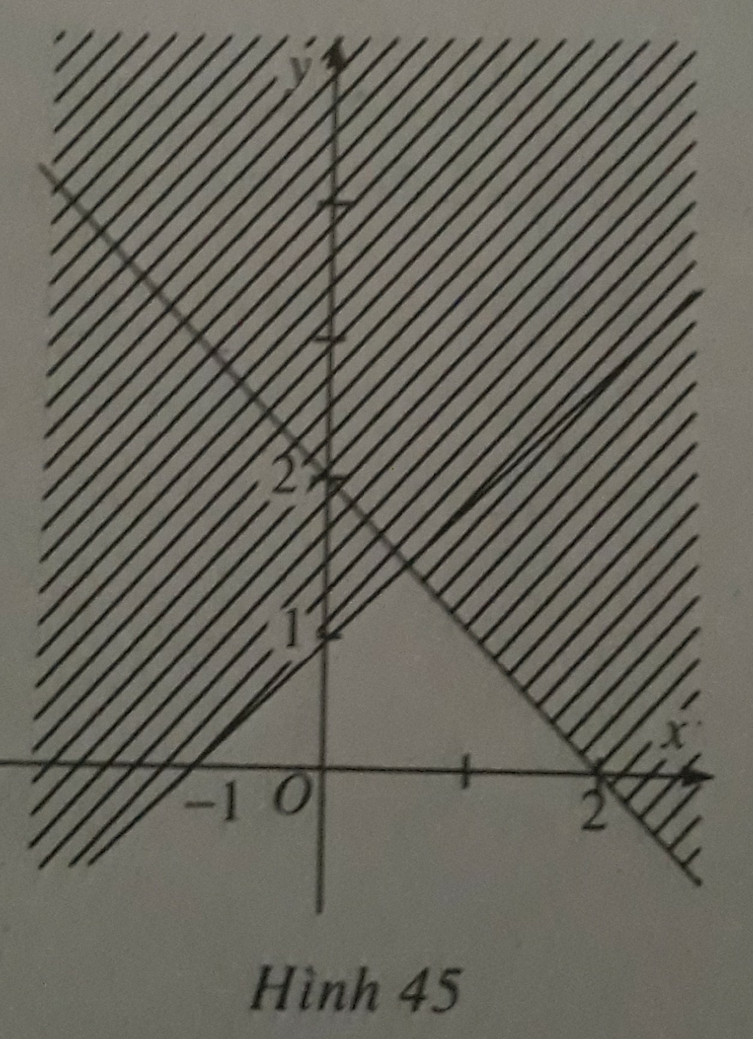
Miền góc không bị gạch được giới hạn bởi hai đường thẳng:
Đường thẳng thứ nhất đi qua hai điểm (3;0) và (0;1) nên có phương trình:
x 3 + y 1 = 1 ⇔ x + 3 y - 3 = 0
Với bờ là đường thẳng x+3y-3=0, theo hình thì phần gạch bỏ không chứa O
Do đó nửa mặt phẳng không gạch (chứa O) với bờ là đường thẳng x+3y-3=0 biểu diễn nghiệm của bất phương trình x+3y-3<0.
Đường thẳng thứ hai đi qua hai điểm (-1;0) và (0;-2) nên có phương trình
x - 1 + y - 2 = 1 ⇔ 2 x + y + 2 = 0
Với bờ là đường thẳng 2x+y+2=0, theo hình thì phần gạch bỏ chứa O
Do đó nửa mặt phẳng không gạch (không chứa O) với bờ là đường thẳng 2x+y+2=0 biểu diễn nghiệm của bất phương trình 2x+y+2<0.
Miền không bị gạch là biểu diễn nghiệm bao gồm cả các đường thẳng, do đó hệ là
x + 3 y + 3 ≤ 0 2 x + y + 2 ≤ 0

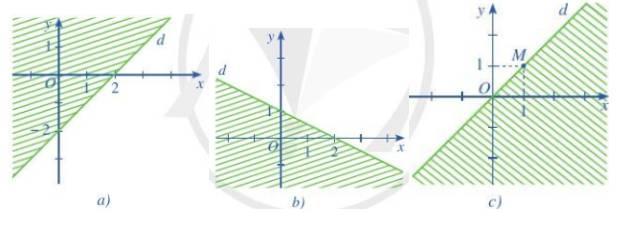
a) Đường thẳng qua điểm (2;0) và (0;-2) nên phương trình đường thẳng là \(x-y-2=0\)
Lấy điểm (3;0) thuộc miền nghiệm ta có 3-0-2=1>0
=> Bất phương trình cần tìm là \(x - y - 2 > 0\)
b) Đường thẳng qua điểm (2;0) và (0;1)
Thay x=2, y=0 vào phương trình \(y = ax + b\) ta được \(0 = 2a + b\)
Thay x=0, y=1 vào phương trình \(y = ax + b\) ta được \(1 = 0.a + b\)
=> \(a = - \frac{1}{2},b = 1\)
=> phương trình đường thẳng là \(y = - \frac{1}{2}x + 1\)
Lấy điểm (3;0) thuộc miền nghiệm ta có \( - \frac{1}{2}x + 1 - y = \frac{{ - 1}}{2} < 0\)
=> Bất phương trình cần tìm là \( - \frac{1}{2}x - y + 1 < 0\)
c) Đường thẳng qua điểm (0;0) và (1;1) nên phương trình đường thẳng là
x-y=0
Lấy điểm (0;1) thuộc miền nghiệm ta có x-y=-1<0
=> Bất phương trình cần tìm là \(x - y < 0\)

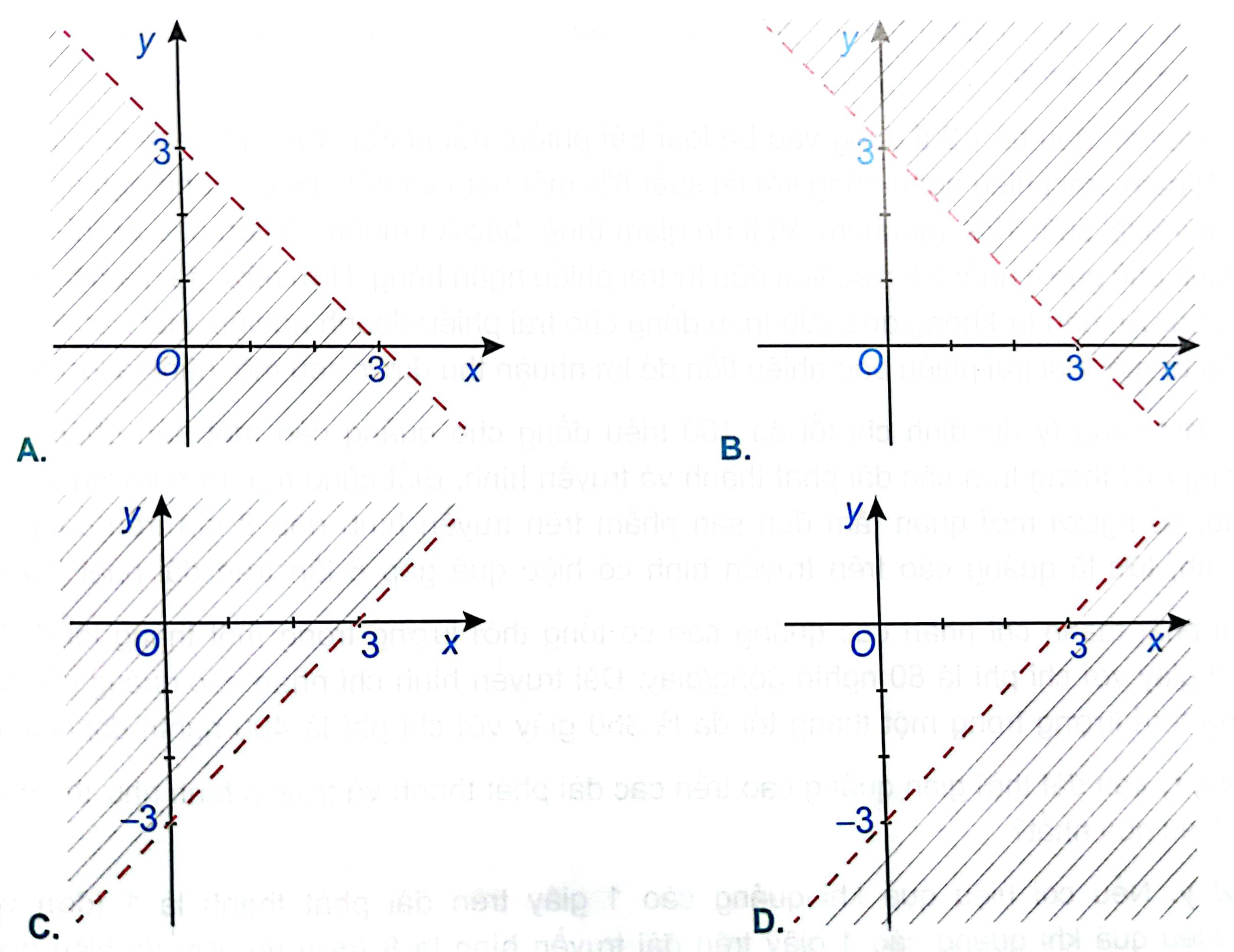
Đường thẳng x-y=3 đi qua điểm A(0;-3)
=> Loại đáp án A, B vì hai đường thẳng trong hình không đi qua A.
Xét điểm O(0;0) ta có: 0-0=0 < 3
=> Điểm O thuộc miền nghiệm của bất phương trình x-y<3
Chọn D
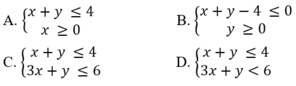
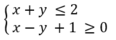 và (x; y) = (1; 0) là một nghiệm của hệ.
và (x; y) = (1; 0) là một nghiệm của hệ.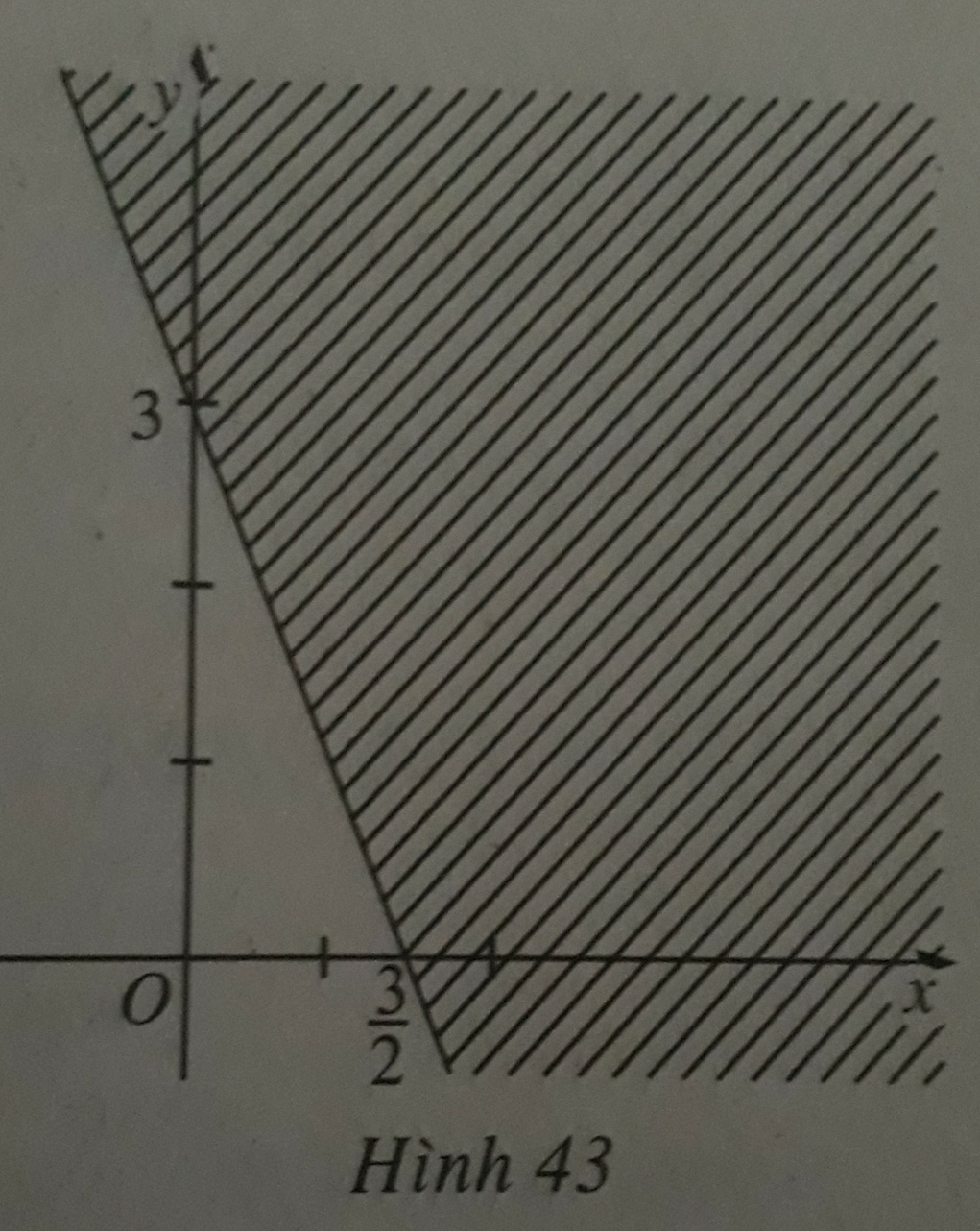


Đáp án: C